语法说明
虽然名字是递归查询,但是严格地讲,整个处理过程是迭代(iteration)而不是递归(recursion),具体语法如下所示【1】:
WITH RECURSIVE cte_name AS(
CTE_query_definition -- non-recursive term
UNION [ALL]
CTE_query definion -- recursive term
) SELECT * FROM cte_name;
with recursive语句由三部分组成【2】:
- non-recursive term —— 递归查询的初始记录
- UNION [ALL] —— 结果集是否需要去重
- recursive term —— 递归查询的具体处理过程,需要在语句中引用cte_name。当上一次迭代返回为空时,整个过程终止。
迭代过程
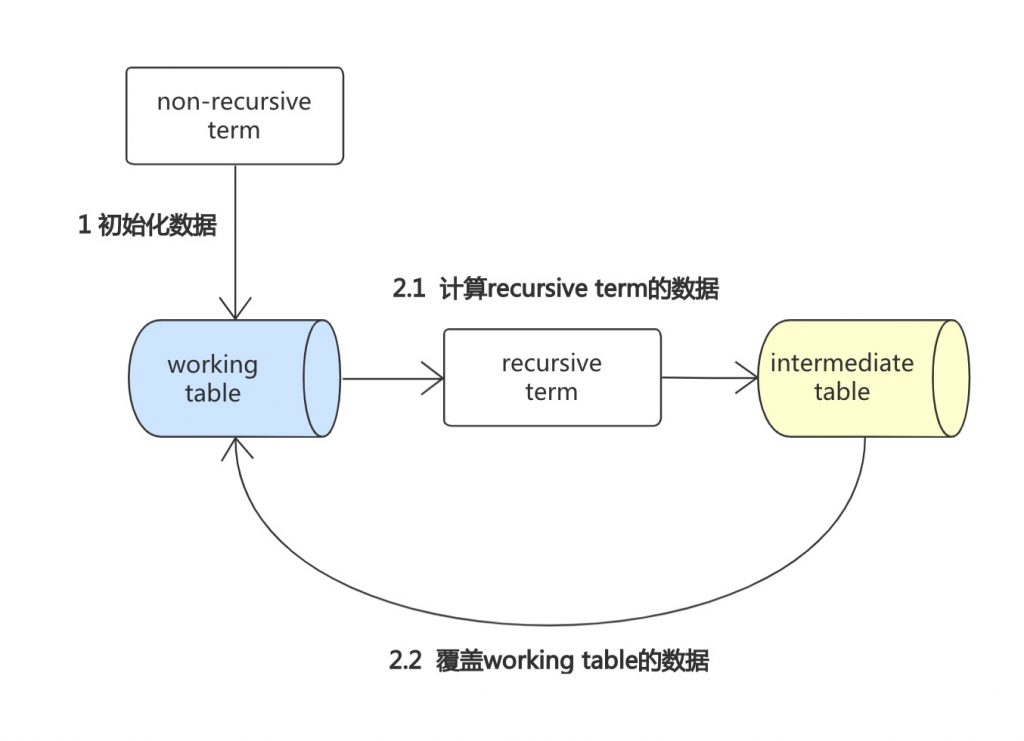
- 计算出non-recursive term的结果(如果是union,需要进行去重),插入到临时的working table中。
- 每一轮迭代,计算recursive term的结果(如果是union,需要进行去重),并用working table替换cte,结果保存到intermediate table中。
- 每一轮迭代结束,将working table的数据替换为intermediate table的数据
- 持续迭代,直到结果为空,过程如下图所示
场景示例
generate series
WITH RECURSIVE t(n) AS (
SELECT 1
UNION ALL
SELECT n+1 FROM t
)
SELECT n FROM t LIMIT 100;
cycle detection
在DAG中,可以获取某个节点的所有下游或上游,比如下图中的graph遍历
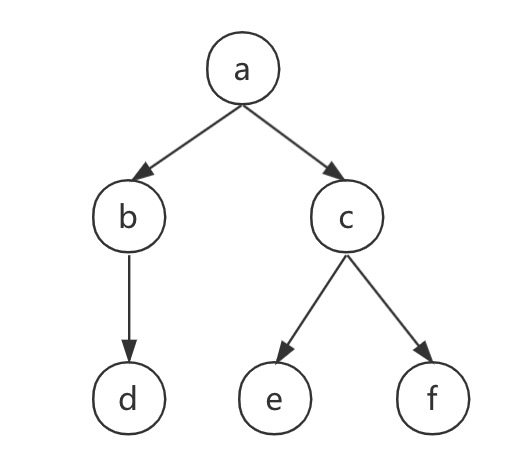
select * From graph;
parent | son
--------+-----
a | b
a | c
b | d
c | e
c | f
(5 rows)
获取a的所有下游以及其深度
WITH RECURSIVE search_graph(son, depth) AS (
SELECT son, 1
FROM graph
WHERE parent = 'a'
UNION ALL
SELECT g.son, sg.depth + 1
FROM graph g, search_graph sg
WHERE g.parent = sg.son
)
SELECT * FROM search_graph;
son | depth
-----+-------
b | 1
c | 1
d | 2
e | 2
f | 2
(5 rows)
默认是广度优先的搜索,如果想要深度优先,需要根据path做个排序
深度优先
WITH RECURSIVE search_graph(son, path, depth) AS (
SELECT son, ARRAY[parent, son] :: text[], 1
FROM graph
WHERE parent = 'a'
UNION ALL
SELECT g.son, path || g.son :: text, sg.depth + 1
FROM graph g, search_graph sg
WHERE g.parent = sg.son
)
SELECT * FROM search_graph order by path;
son | path | depth
-----+---------+-------
b | {a,b} | 1
d | {a,b,d} | 2
c | {a,c} | 1
e | {a,c,e} | 2
f | {a,c,f} | 2
(5 rows)
如果形成了环,则迭代过程无法结束,需要能够检测出环
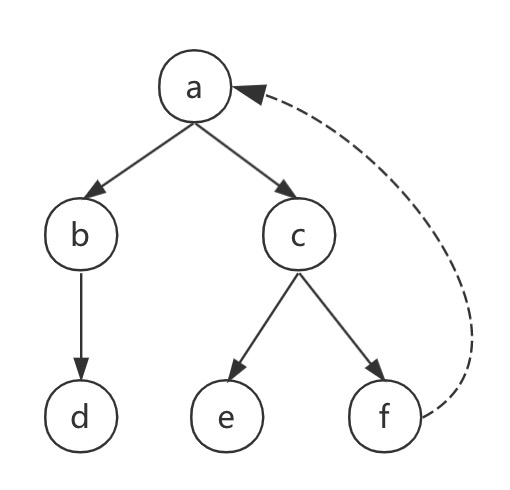
select * from graph;
parent | son
--------+-----
a | b
a | c
b | d
c | e
c | f
f | a
(6 rows)
WITH RECURSIVE search_graph(son, path, depth, cycle) AS (
SELECT son, ARRAY[parent, son] :: text[], 1, false
FROM graph
WHERE parent = 'a'
UNION ALL
SELECT g.son, path || g.son :: text, sg.depth + 1, g.son = ANY(path)
FROM graph g, search_graph sg
WHERE g.parent = sg.son AND NOT cycle
)
SELECT * FROM search_graph;
son | path | depth | cycle
-----+-----------+-------+-------
b | {a,b} | 1 | f
c | {a,c} | 1 | f
d | {a,b,d} | 2 | f
e | {a,c,e} | 2 | f
f | {a,c,f} | 2 | f
a | {a,c,f,a} | 3 | t
(6 rows)
finding shortest path
对于travelling salesman problem【3】,可以通过with recursive query穷举出所有可能的路径,再从结果中找出最短路径。首先是准备相关数据,并创建对应的function【4】。
create table places as (
select
'Seattle' as name, 47.6097 as lat, 122.3331 as lon
union all select 'San Francisco', 37.7833, 122.4167
union all select 'Austin', 30.2500, 97.7500
union all select 'New York', 40.7127, 74.0059
union all select 'Boston', 42.3601, 71.0589
union all select 'Chicago', 41.8369, 87.6847
union all select 'Los Angeles', 34.0500, 118.2500
union all select 'Denver', 39.7392, 104.9903
)
两点之间的距离计算
create or replace function lat_lon_distance(
lat1 float, lon1 float, lat2 float, lon2 float
) returns float as $$
declare
x float = 69.1 * (lat2 - lat1);
y float = 69.1 * (lon2 - lon1) * cos(lat1 / 57.3);
begin
return sqrt(x * x + y * y);
end
$$ language plpgsql
首先计算出某个城市出发的不重复的所有路径
with recursive travel(places_chain, last_lat, last_lon,
total_distance, num_places) as (
select array[name]::text[], lat, lon, 0::float, 1
from places
where name = 'San Francisco'
union all
select travel.places_chain || places.name::text,
places.lat,
places.lon,
travel.total_distance + lat_lon_distance(last_lat, last_lon, places.lat, places.lon),
travel.num_places + 1
from
places, travel
where NOT places.name = ANY(travel.places_chain)
)
再回到起点,从而计算出全部路径的长度,并进行排序
select
travel.places_chain || places.name as full_path,
total_distance + lat_lon_distance(
travel.last_lat, travel.last_lon,
places.lat, places.lon) as final_dist
from travel, places
where
travel.num_places = 8
and places.name = 'San Francisco'
order by 2
limit 1
full_path | final_dist
-------------------------------------------------------------------------------------------------+------------------
{"San Francisco",Seattle,Denver,Chicago,Boston,"New York",Austin,"Los Angeles","San Francisco"} | 6670.83798218894
(1 row)
预计完成时间
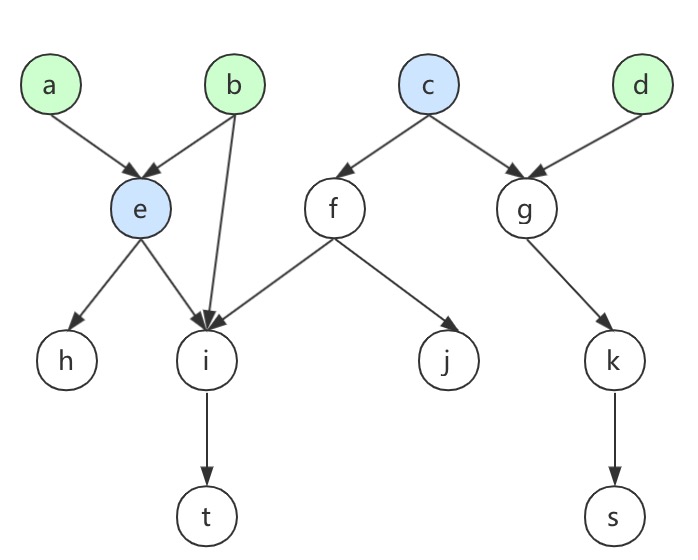
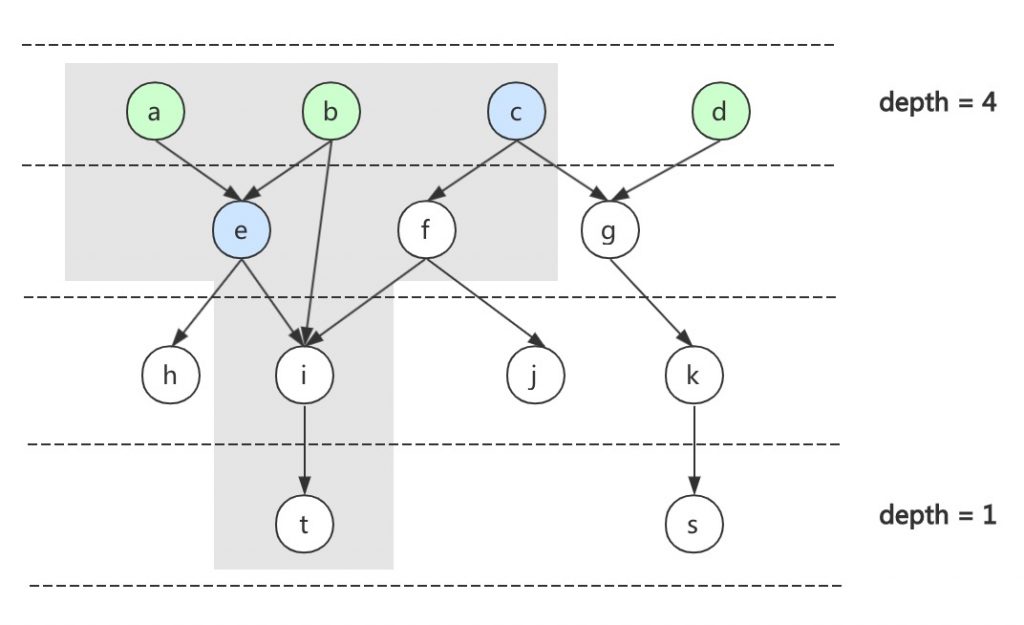
如果现在想预测上图中节点T的完成时间,首先构造出节点之间的依赖关系,同时预先计算出每个节点的预计运行时间。
select * from graph;
parent | son
--------+-----
a | e
b | e
c | f
c | g
d | g
e | h
e | i
f | i
f | j
g | k
i | t
k | s
b | i
(13 rows)
select * from node;
id | status | start_time | end_time | avg_duration
----+---------+------------+----------+--------------
a | success | 0 | 10 | 9
b | success | 0 | 9 | 9
e | running | 10 | | 12
c | running | 0 | | 20
d | success | 0 | 15 | 16
f | waiting | | | 5
g | waiting | | | 6
h | waiting | | | 16
i | waiting | | | 13
j | waiting | | | 20
k | waiting | | | 14
t | waiting | | | 3
s | waiting | | | 11
(13 rows)
基本思路就是先找出T节点的所有上游,即下图中的灰色部分,并将这些上游进行分层。
WITH RECURSIVE search_graph(node, depth) AS ( -- 备注1,获取上游节点
SELECT son, 1
FROM graph
WHERE son = 't'
UNION ALL
SELECT g.parent, sg.depth + 1
FROM graph g, search_graph sg
WHERE g.son = sg.node
),
node_depth_mapping AS ( -- 备注2,节点分层
SELECT node as id, max(depth) as depth
FROM search_graph
GROUP BY node
),
finish_time(id, status, start_time, end_time, avg_duration) AS (
SELECT
node.id,
node.status,
node.start_time,
case
when node.status = 'success' then node.end_time
when node.status = 'running' then node.start_time + node.avg_duration
end as end_time,
node.avg_duration,
array [node.id] ::text [] as path,
mapping.depth
FROM
node
JOIN node_depth_mapping mapping ON node.id = mapping.id
WHERE
mapping.depth = (select max(depth) from node_depth_mapping)-- 备注3,先获取最大层
UNION ALL
select
id,
status,
start_time,
end_time,
avg_duration,
path,
depth
from
(
WITH inner_table as (select * From finish_time) -- 备注4,为了绕过PG的限制
SELECT
node.id,
node.status,
case
when node.start_time is not null then node.start_time
else parent_finish.end_time
end as start_time,
case
when node.status = 'success' then node.end_time
when node.status = 'running' then node.start_time + node.avg_duration
else case
when node.start_time is not null then node.start_time
else parent_finish.end_time
end + node.avg_duration
end as end_time, -- 备注5,预测下游节点的产出时间
node.avg_duration,
path || node.id::text as path, -- 备注6,记录从顶点到目标的路径
mapping.depth,
row_number() over( -- 备注7,根据产出时间倒序排序
partition by node.id
order by
case
when node.status = 'success' then node.end_time
when node.status = 'running' then node.start_time + node.avg_duration
else case
when node.start_time is not null then node.start_time
else parent_finish.end_time
end + node.avg_duration
end desc
) as rk
FROM
node
JOIN node_depth_mapping mapping ON node.id = mapping.id
-- 备注8,每次迭代处理下一层
AND mapping.depth = (select depth from inner_table limit 1) - 1
JOIN graph ON node.id = graph.son
JOIN inner_table parent_finish ON graph.parent = parent_finish.id
) a
where
a.rk = 1
)
SELECT * FROM finish_time;
针对上面SQL的备注解释:
- 先通过递归查询,获取T节点的所有上游,并记录下层数
- 上游节点可能会有多个层数,比如B节点,需要取最大的层数,从而将节点分层
- 递归查询的non-recursive部分,先处理最大层数的节点
- recursive部分,不能出现多次cte name,所以通过with语句绕开这个限制【5】
- 预测下游节点的产出,根据不同的状态会有不同的算法
- 记录下从顶点到目标的路径
- 仅需要保留最迟产出的那条路径
- 递归查询的recursive部分,每次处理下一个层数
最终的结果如下表所示:
id | status | start_time | end_time | avg_duration | path | depth
----+---------+------------+----------+--------------+-----------+-------
a | success | 0 | 10 | 9 | {a} | 4
b | success | 0 | 9 | 9 | {b} | 4
c | running | 0 | 20 | 20 | {c} | 4
e | running | 10 | 22 | 12 | {a,e} | 3
f | waiting | 20 | 25 | 5 | {c,f} | 3
i | waiting | 25 | 38 | 13 | {c,f,i} | 2
t | waiting | 38 | 41 | 3 | {c,f,i,t} | 1
(7 rows)
从结果中可以计算出t节点的预计完成时间,以及关键的产出路径