第一篇中的解法过于简单,第二篇中的解法又过于粗暴,有没有更优的解法呢?搜索了下,还真有这样的算法,就是Crook’s Algorithm。
Crook’s Algorithm
rtx090400460p该算法中提及的方法也比较好懂,在实际解题时也经常使用的方法。就是每个未知位置先填上所有可能的候选数字,再观察同一行/列/方格中的候选数字组合。如果观察到候选数字组合中的数量=对应空格数量,则可以排除掉其他空格的数字候选。
以下图的例子举例,C6和C9的候选数字是[6,7],则同一行其他的候选不可能是[6,7],可以排除掉这些候选,从而确定C1的数字为8。
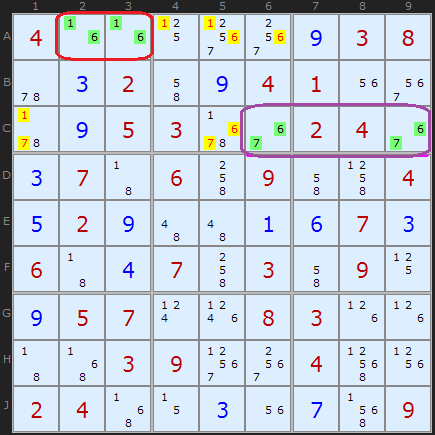
还有稍微有些变化的例子,就是三个空格的候选分别是{1,4} {1,7} {1,4,7},则[1,4,7]只能出现在这三个空格内,不能出现在其他空格了。论文中将这种组合称之为Preemptive set,下面我们就看下如何寻找。
Find Preemptive Sets
sudoku.com找一个master级别的数独
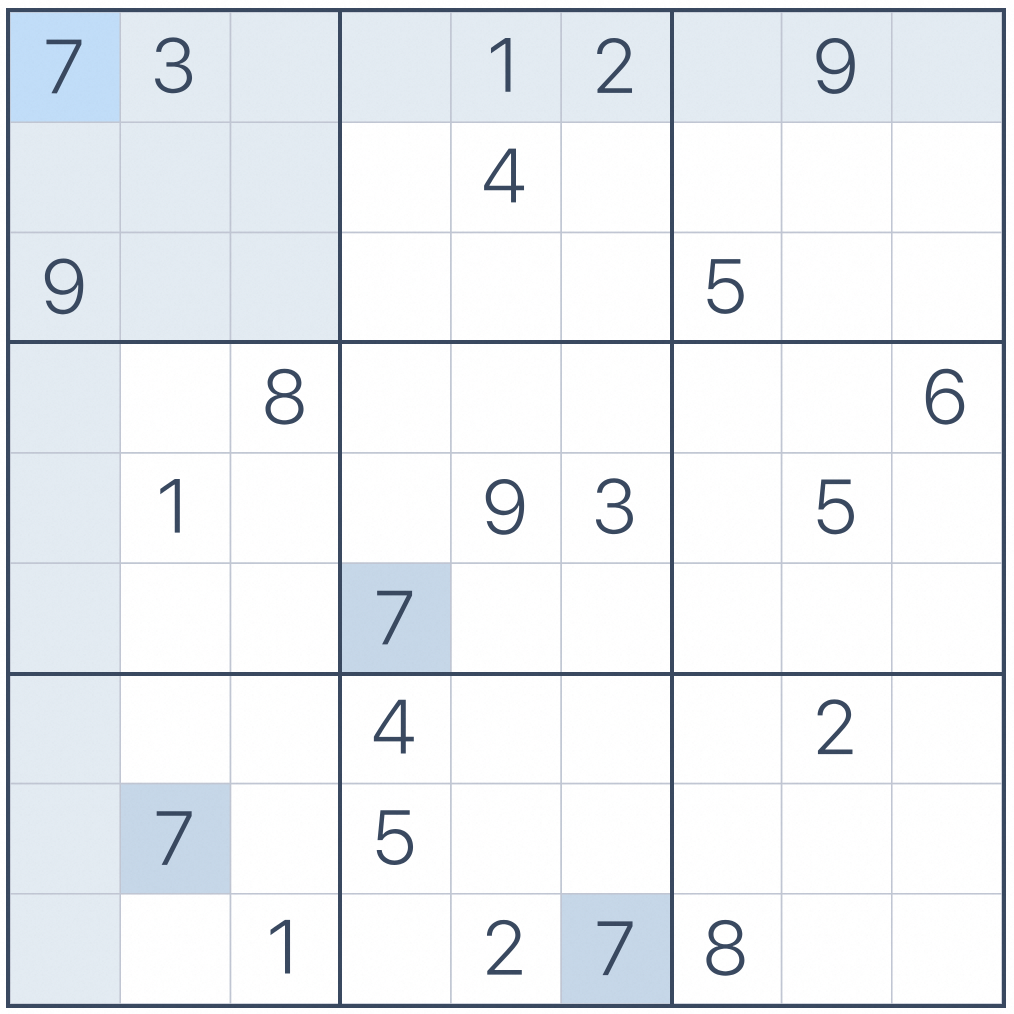
经过简单的计算后,可以得出如下的结果
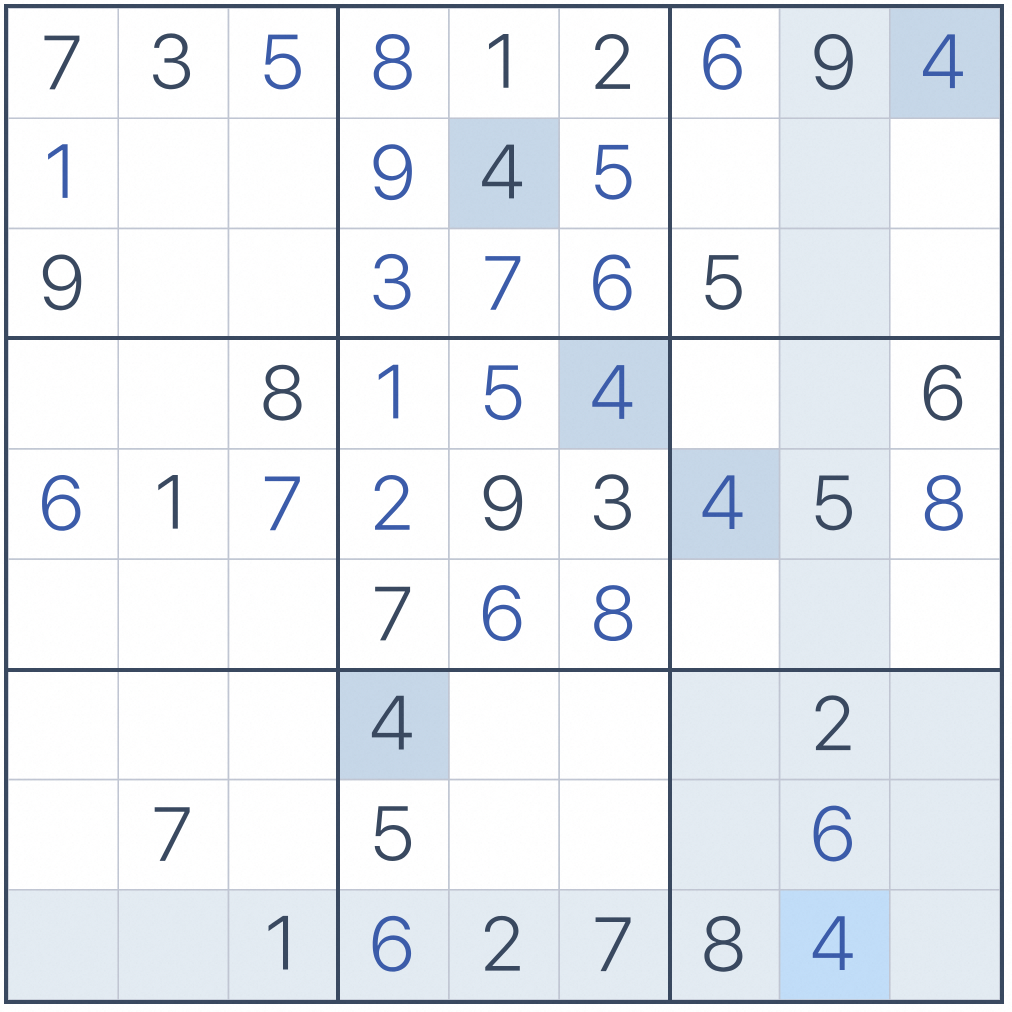
下面就需要计算出Preemptive set
-- find candidates for each number
cell_num_array(_grid, _row, _col, num_arr) AS (
SELECT _grid, _row, _col, array_agg(num order by num) as num_arr
FROM num_cell
GROUP BY _grid, _row, _col
),
-- union of each num_arr. For example {1,3} | {1,7} = {1,3,7}
cell_num_array_union(_grid, _row, _col, num_arr) AS (
SELECT DISTINCT *
FROM (
SELECT z._grid, z._row, z._col, (x.num_arr | y.num_arr)
FROM (SELECT DISTINCT num_arr FROM cell_num_array) x,
(SELECT DISTINCT num_arr FROM cell_num_array) y,
cell_num_array z
WHERE x.num_arr != y.num_arr
AND (x.num_arr | y.num_arr) @> z.num_arr
UNION ALL
SELECT _grid, _row, _col, num_arr FROM cell_num_array
) t
),
-- find preemptive sets, GROUP BY ROW
num_array_cell_by_row(num_arr, _row, cell_arr) AS (
SELECT num_arr, _row, array_agg(_row * 10 + _col)
FROM cell_num_array_union
GROUP BY num_arr, _row
HAVING #num_arr = # (array_agg(_row * 10 + _col)::integer[])
),
-- find preemptive sets, GROUP BY COL
num_array_cell_by_col(num_arr, _col, cell_arr) AS (
SELECT num_arr, _col, array_agg(_row * 10 + _col)
FROM cell_num_array_union
GROUP BY num_arr, _col
HAVING #num_arr = # (array_agg(_row * 10 + _col)::integer[])
),
-- find preemptive sets, GROUP BY GRID
num_array_cell_by_grid(num_arr, _grid, cell_arr) AS (
SELECT num_arr, _grid, array_agg(_row * 10 + _col)
FROM cell_num_array_union
GROUP BY num_arr, _grid
HAVING #num_arr = # (array_agg(_row * 10 + _col)::integer[])
),
通过计算,发现{8,6}{8,7}{8,9}三个空格组成了preemptive sets [1,3,9],所以{8,5}空格可以去掉候选数字3,因此确定了该空格的数字8。
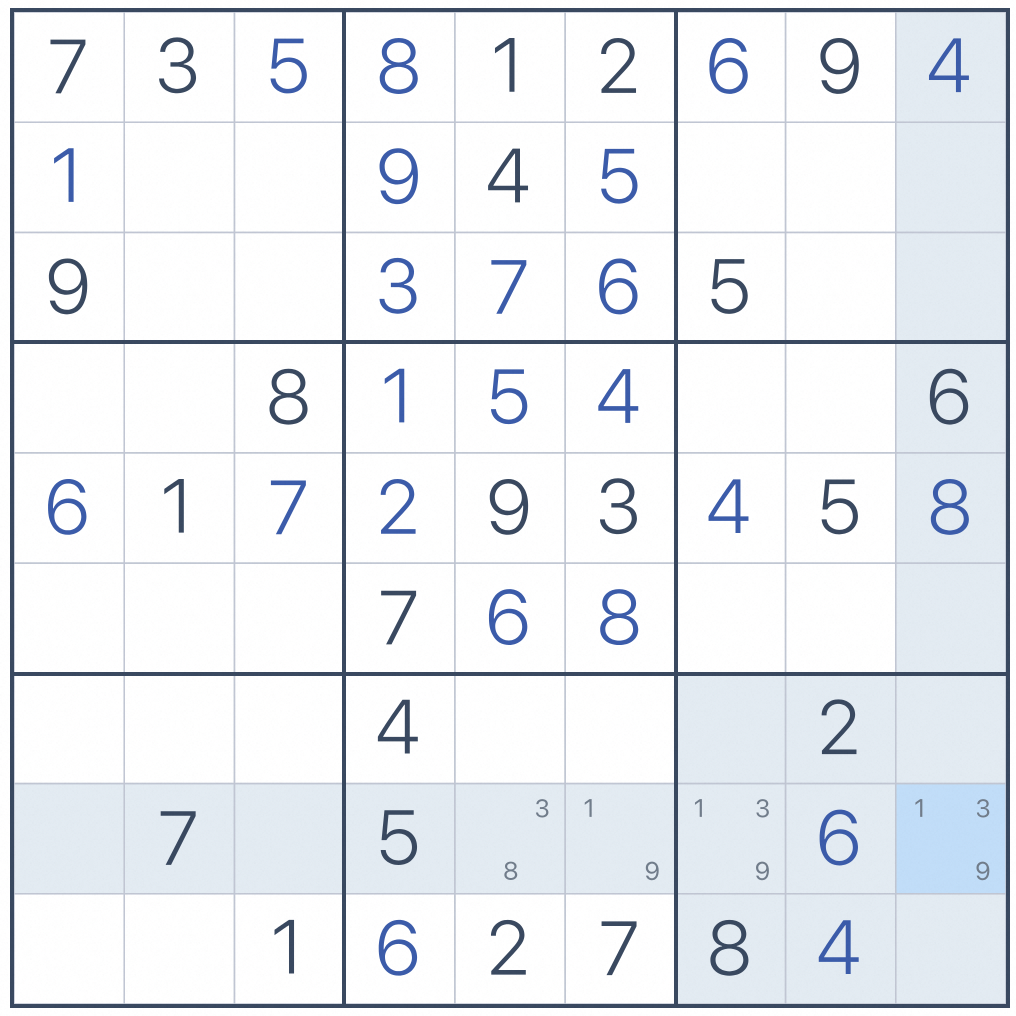
最终SQL
WITH RECURSIVE sudoku_result(c) AS (
-- original problem
SELECT c :: text
FROM sudoku
UNION ALL
SELECT string_agg(num :: text, '' order by _col) :: text as c
FROM (
-- find num using cell_to_num OR num_to_cell
SELECT _row, _col, case when # valid_arr = 1 then valid_arr[1] when valid_num IS NOT NULL then valid_num else num end as num
FROM (
-- split to 81 cells with grid/row/col proeperties
WITH all_cell(_grid, _row, _col, num) AS (
SELECT ceil(rn / 3.0) * 10 + ceil(t.x / 3.0) as _grid, rn as _row, t.x as _col, substr(s.c, t.x, 1) :: integer as num
FROM (
SELECT c,row_number() over () as rn
FROM sudoku_result
) s, all_num t
),
-- find valid numbers in a cell, just filter forbidden numbers of same grid/row/col
cell_to_num(_row, _col, forbid_arr) AS (
SELECT y._row, y._col, uniq(array_agg(x.num)) as forbid_arr
FROM all_cell x
JOIN all_cell y
ON x.num != 0 AND y.num = 0
WHERE x._grid = y._grid
OR x._row = y._row
OR x._col = y._col
GROUP BY y._row, y._col
),
-- find valid cells for a number
num_cell(num, _grid, _row, _col) AS (
SELECT num, _grid, _row, _col
FROM (
SELECT all_num.x as num, y._grid, y._row, y._col, case when x._grid = y._grid OR x._row = y._row OR x._col = y._col THEN 0 ELSE 1 end as flag
FROM all_num
JOIN all_cell x
ON all_num.x = x.num
JOIN all_cell y
ON y.num = 0
) s
GROUP BY num, _grid, _row, _col
HAVING min(flag) = 1
),
-- find candidates for each number
cell_num_array(_grid, _row, _col, num_arr) AS (
SELECT _grid, _row, _col, array_agg(num order by num) as num_arr
FROM num_cell
GROUP BY _grid, _row, _col
),
-- union of each num_arr. For example {1,3} | {1,7} = {1,3,7}
cell_num_array_union(_grid, _row, _col, num_arr) AS (
SELECT DISTINCT *
FROM (
SELECT z._grid, z._row, z._col, (x.num_arr | y.num_arr)
FROM (SELECT DISTINCT num_arr FROM cell_num_array) x,
(SELECT DISTINCT num_arr FROM cell_num_array) y,
cell_num_array z
WHERE x.num_arr != y.num_arr
AND (x.num_arr | y.num_arr) @> z.num_arr
UNION ALL
SELECT _grid, _row, _col, num_arr FROM cell_num_array
) t
),
-- find preemptive sets, GROUP BY ROW
num_array_cell_by_row(num_arr, _row, cell_arr) AS (
SELECT num_arr, _row, array_agg(_row * 10 + _col)
FROM cell_num_array_union
GROUP BY num_arr, _row
HAVING #num_arr = # (array_agg(_row * 10 + _col)::integer[])
),
-- find preemptive sets, GROUP BY COL
num_array_cell_by_col(num_arr, _col, cell_arr) AS (
SELECT num_arr, _col, array_agg(_row * 10 + _col)
FROM cell_num_array_union
GROUP BY num_arr, _col
HAVING #num_arr = # (array_agg(_row * 10 + _col)::integer[])
),
-- find preemptive sets, GROUP BY GRID
num_array_cell_by_grid(num_arr, _grid, cell_arr) AS (
SELECT num_arr, _grid, array_agg(_row * 10 + _col)
FROM cell_num_array_union
GROUP BY num_arr, _grid
HAVING #num_arr = # (array_agg(_row * 10 + _col)::integer[])
),
-- filter result by using preemptive sets
num_cell_filter(num, _grid, _row, _col) AS (
SELECT x.num, x._grid, x._row, x._col
FROM num_cell x
LEFT JOIN num_array_cell_by_row r
ON x._row = r._row
AND x.num = ANY(r.num_arr)
AND NOT ((x._row * 10 + x._col) = ANY(r.cell_arr))
LEFT JOIN num_array_cell_by_col c
ON x._col = c._col
AND x.num = ANY(c.num_arr)
AND NOT ((x._row * 10 + x._col) = ANY(c.cell_arr))
LEFT JOIN num_array_cell_by_grid g
ON x._grid = g._grid
AND x.num = ANY(g.num_arr)
AND NOT ((x._row * 10 + x._col) = ANY(g.cell_arr))
WHERE r.num_arr IS NULL
AND c.num_arr IS NULL
AND g.num_arr iS NULL
),
-- find valid cells for a number, only keep records with only one candidate cell for a number
num_to_cell(num, _row, _col) AS (
SELECT num_cell_filter.num, num_cell_filter._row, num_cell_filter._col
FROM num_cell_filter
LEFT JOIN (select _grid, num from num_cell_filter group by _grid, num having count(*) = 1) g
ON num_cell_filter.num = g.num
AND num_cell_filter._grid = g._grid
LEFT JOIN (select _row, num from num_cell_filter group by _row, num having count(*) = 1) r
ON num_cell_filter.num = r.num
AND num_cell_filter._row = r._row
LEFT JOIN (select _col, num from num_cell_filter group by _col, num having count(*) = 1) c
ON num_cell_filter.num = c.num
AND num_cell_filter._col = c._col
WHERE g.num is not null OR r.num is not null OR c.num is not null
)
-- condition for recursive query terminated. No blank cells.
SELECT x.*, case when x.num = 0 then all_arr.x - y.forbid_arr end as valid_arr, z.num as valid_num
FROM all_cell x
JOIN all_arr
ON 1=1
LEFT JOIN cell_to_num y
ON x._row = y._row
AND x._col = y._col
LEFT JOIN num_to_cell z
ON x._row = z._row
AND x._col = z._col
WHERE exists (select * From all_cell where num = 0)
) s1 order by _row
) s2
GROUP BY _row
),
-- all numbers as integer array
all_arr(x) AS (
SELECT '{1,2,3,4,5,6,7,8,9}' :: integer[]
),
-- all numbers as multiple rows
all_num(x) AS (
SELECT unnest(x) from all_arr
)
SELECT * FROM sudoku_result;
最终结果如下:
c1 | c2 | c3
-----+-----+-----
735 | 812 | 694
186 | 945 | 237
924 | 376 | 581
--- | --- | ---
298 | 154 | 376
617 | 293 | 458
543 | 768 | 912
--- | --- | ---
869 | 431 | 725
472 | 589 | 163
351 | 627 | 849
(11 rows)