上一篇文章的解法,是按照正向解题的思路去尝试解决。然而这种解法只能解决简单难度的数独,如果是大师级难度,则会遇到阻塞。比如下图中的这个大师级难度的数独:
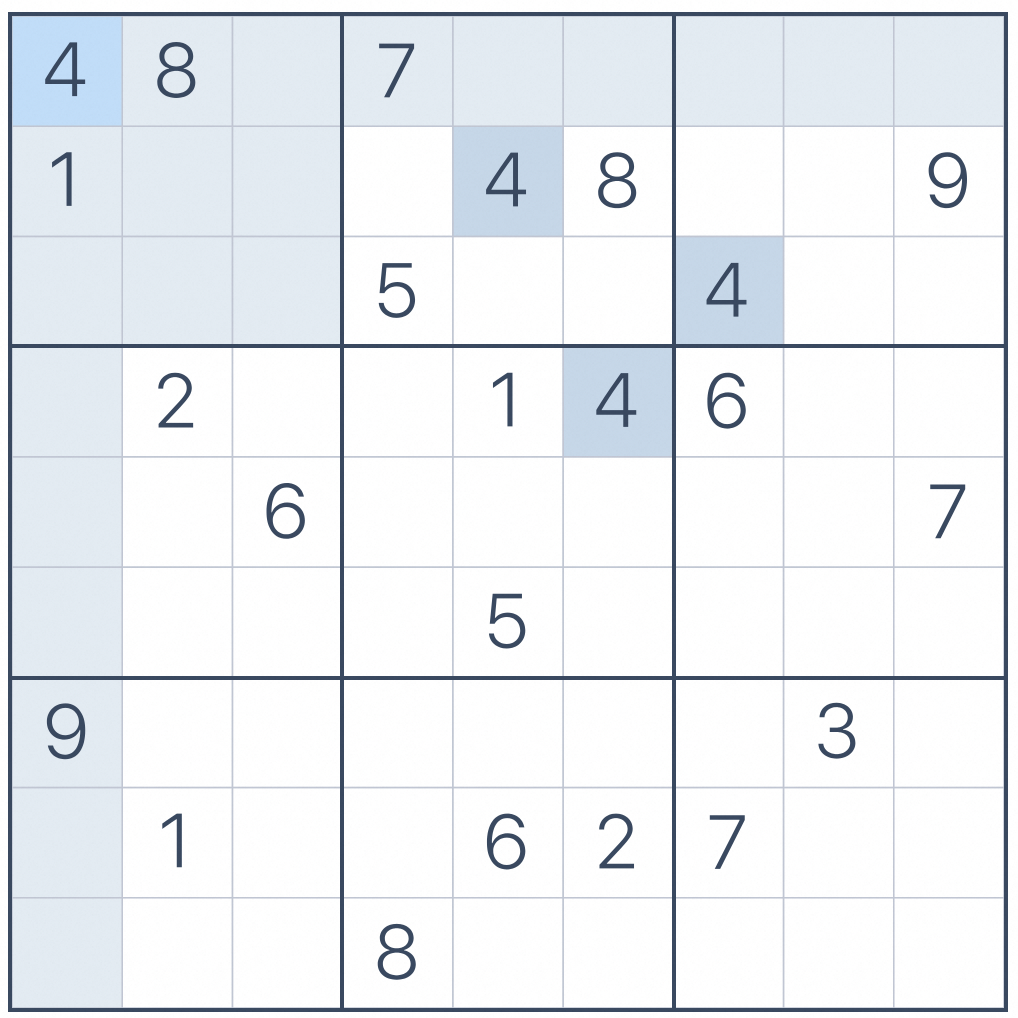
运行SQL后,由于无法找到唯一候选,只能解决到如下图中的阶段
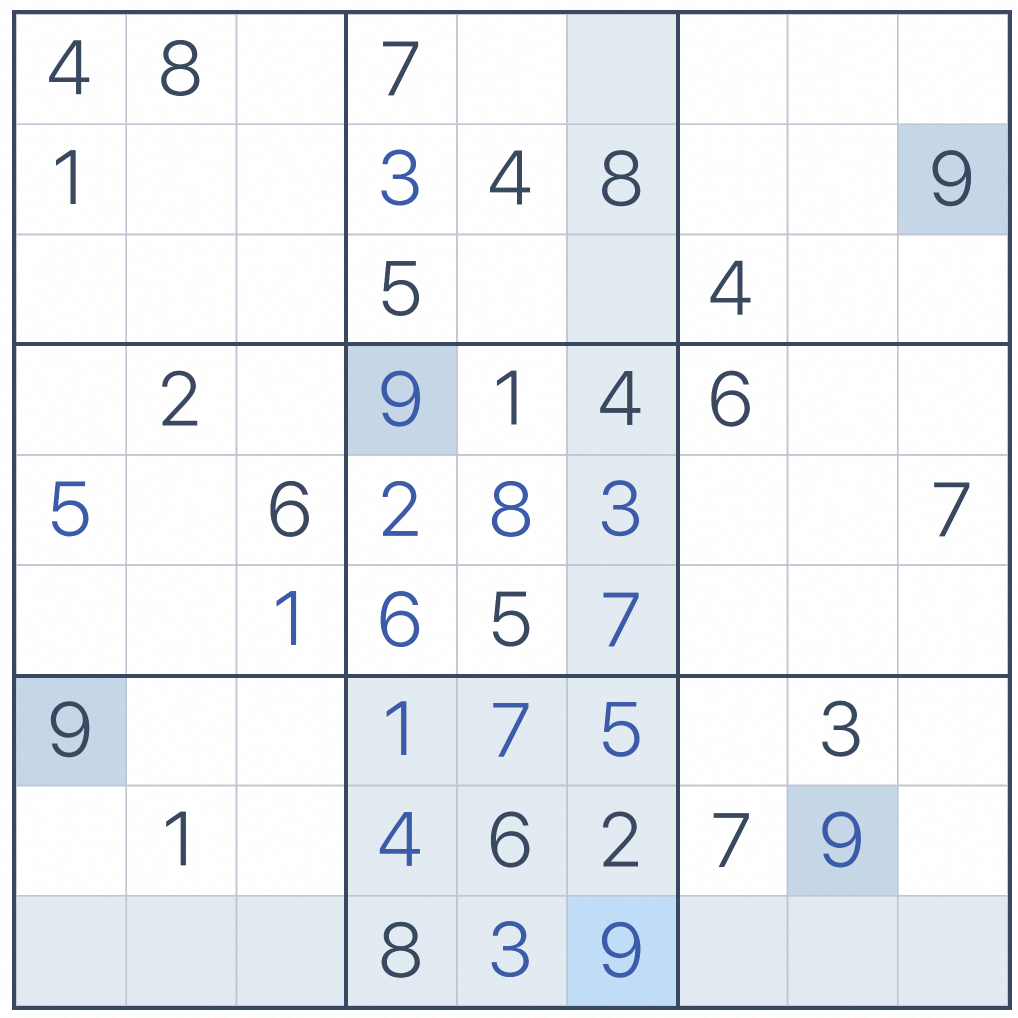
因此这里可以采用暴力的穷举方式,来找到最终的解。
穷举法
将所有数字合并到一起,形成一个大的字符串。每次迭代都寻找下一个为0的位置,并从1-9的数字逐个尝试替换,直到所有的0都被替换为1-9的数字为止。
因此数独初始有多少个空位,就需要迭代多少次。每次迭代产出的记录数也是指数增长,所以需要每次迭代都过滤掉无效记录。无效记录就是违反数独的行、列、方格的数字唯一性。
SELECT substring(all_rows from 1 for last_index - 1)
|| m.x ||
substring(all_rows from last_index + 1) as all_rows,
position('0' in substring(all_rows from last_index + 1)) + last_index as last_index
FROM sudoku_result, all_num m
过滤记录
根据last_index,找出该空位所在的行、列、方格,并寻找同行、同列、同方格中是否有数字相同的记录,如果有,则说明该记录无效,直接过滤掉即可。
行过滤
行过滤比较简单,根据last_index求出所在行的起点index,再加上[1-9],就是所在行的所有位置。
substring(all_rows from (floor((last_index - 1) / 9.0) * 9 + n.x) :: INTEGER for 1) :: INTEGER
postgres=> select floor((29 - 1) / 9.0) * 9 + n.x from (select unnest('{1,2,3,4,5,6,7,8,9}'::integer[]) as x) n;
?column?
----------
28
29
30
31
32
33
34
35
36
(9 rows)
列过滤
列过滤也比较简单,根据last_index mod 9求出第几列,再加上[1-9]行,就是所在列的所有位置。
substring(all_rows from (mod(last_index - 1, 9) + (n.x - 1) * 9 + 1) :: INTEGER for 1) :: INTEGER
postgres=> select mod(57 - 1, 9) + (n.x - 1) * 9 + 1 from (select unnest('{1,2,3,4,5,6,7,8,9}'::integer[]) as x) n;
?column?
----------
3
12
21
30
39
48
57
66
75
(9 rows)
方格过滤
3*3的方格过滤比较复杂,其index是不连续的,如下图所示:
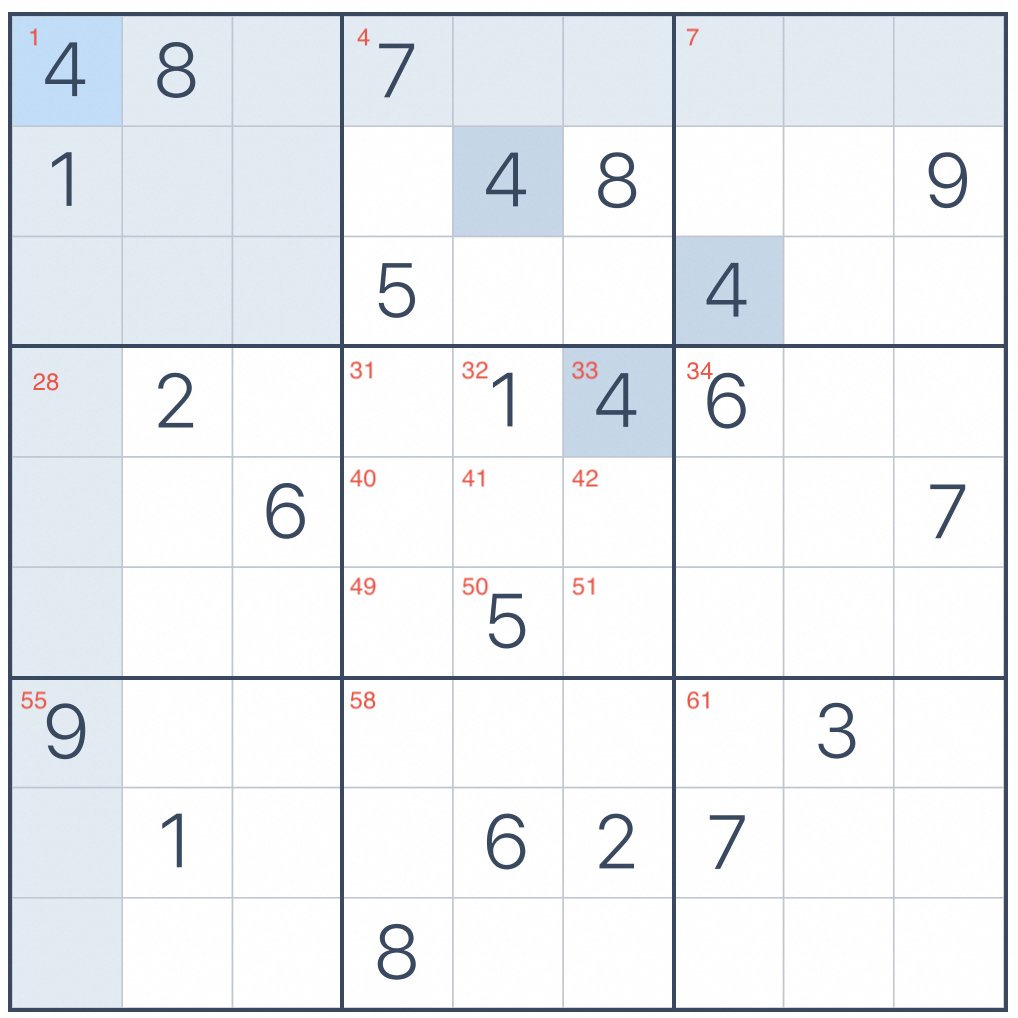
因此第一步需要找到3*3方格的起始位置,[1, 4, 7, 28, 31, 34, 55, 58, 61]
floor((last_index - 1) / 27.0) * 27 + mod(floor((last_index - 1) / 3.0), 3) * 3 + 1
postgres=> select floor((41 - 1) / 27.0) * 27 + mod(floor((41 - 1) / 3.0), 3) * 3 + 1;
?column?
----------
31
(1 row)
postgres=>
postgres=> select floor((80 - 1) / 27.0) * 27 + mod(floor((80 - 1) / 3.0), 3) * 3 + 1;
?column?
----------
61
(1 row)
再加上[1-9],每三个就要换一行,因此得出如下最终的公式:
floor((last_index - 1) / 27.0) * 27 + mod(floor((last_index - 1) / 3.0), 3) * 3 + floor((n.x - 1) / 3.0) * 9 + mod((n.x - 1), 3) + 1
postgres=> select floor((42 - 1) / 27.0) * 27 + mod(floor((42 - 1) / 3.0), 3) * 3 + floor((n.x - 1) / 3.0) * 9 + mod((n.x - 1), 3) + 1 from (select unnest('{1,2,3,4,5,6,7,8,9}'::integer[]) as x) n;
?column?
----------
31
32
33
40
41
42
49
50
51
(9 rows)
最终SQL
WITH RECURSIVE sudoku_result(all_rows, last_index) AS (
-- original problem
SELECT string_agg(c :: text, '') as all_rows, position('0' in string_agg(c :: text, '')) as last_index
FROM sudoku
UNION ALL
SELECT substring(all_rows from 1 for last_index - 1)
|| m.x ||
substring(all_rows from last_index + 1) as all_rows,
position('0' in substring(all_rows from last_index + 1)) + last_index as last_index
FROM sudoku_result, all_num m
WHERE last_index > 0
AND NOT EXISTS (
SELECT x
FROM all_num n
WHERE substring(all_rows from (floor((last_index - 1) / 9.0) * 9 + n.x) :: INTEGER for 1) :: INTEGER = m.x
OR substring(all_rows from (mod(last_index - 1, 9) + (n.x - 1) * 9 + 1) :: INTEGER for 1) :: INTEGER = m.x
OR substring(all_rows from (floor((last_index - 1) / 27.0) * 27 + mod(floor((last_index - 1) / 3.0), 3) * 3 + floor((n.x - 1) / 3.0) * 9 + mod((n.x - 1), 3) + 1) :: INTEGER for 1) :: INTEGER = m.x
)
),
-- all numbers as integer array
all_arr(x) AS (
SELECT '{1,2,3,4,5,6,7,8,9}' :: integer[]
),
-- all numbers as multiple rows
all_num(x) AS (
SELECT unnest(x) from all_arr
)
SELECT * FROM sudoku_result;
最终计算出了结果,但是代价还是比较大的,迭代了58次,产生了11w条记录
postgres=> select count(*) from sudoku_all;
count
--------
116326
(1 row)
postgres=> select count(distinct last_index) from sudoku_all;
count
-------
58
(1 row)
postgres=> select * from sudoku_all limit 10 offset 116320;
all_rows | last_index
-----------------------------------------------------------------------------------+------------
485796321172348569639521478728914653546283917391657284964175832813462795257800000 | 77
485796321172348569639521478728914653546283917391657284964175832813462795257830000 | 78
485796321172348569639521478728914653546283917391657284964175832813462795257839000 | 79
485796321172348569639521478728914653546283917391657284964175832813462795257839100 | 80
485796321172348569639521478728914653546283917391657284964175832813462795257839140 | 81
485796321172348569639521478728914653546283917391657284964175832813462795257839146 | 81
(6 rows)