《hands-on ml》Chapter 4 – 天枢星的博客

Training Models

线性回归（Linear Regression）

线性回归模型

回顾之前的例子，幸福指数与人均GDP呈线性正相关。一个线性回归模型，就是在输入特征上加权之后相加，再加上一个常量，称之为bias term（intercept term）。用方程来表示，就是

\hat{y} = \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n

用向量方式来表达就是

\hat{y} = h_\theta(x) = \theta^T\cdot\mathrm{x}

y为模型的预测值。
θ 就是模型的参数向量，包括bias term θ₀，以及特征上的权重θ₁到θ_n。
θ^T，就是θ向量的转置，从(n+1) * 1变化为1 * (n+1)
x是实例的特征向量，包含从x₀到x_n，其中x₀永远为1。
θ^T ^. x，是两个向量的点积（dot product）。
h_θ就是基于参数θ的假设方程。

点积的定义如下

\mathrm{a}\cdot\mathrm{b} = \sum_{i=1}^{n}a_ib_i=a_1b_1+a_2b_2+...+a_nb_n \\ \mathrm{a}\cdot\mathrm{b} = \mathrm{a}^\mathrm{T}\mathrm{b}

为了评估模型的表现，可以用Root Mean Square Error（RMSE）

RMSE((\mathrm{X},h)) = \sqrt{\frac{1}{m}\sum_{i=1}^{m}(h(\mathrm{x}^{(i)}) - y^{(i)})^2}

为了节约计算，也可以用更简单的Mean Square Error（MSE）

MSE((\mathrm{X},h)) = \frac{1}{m}\sum_{i=1}^{m}(h(\mathrm{x}^{(i)}) - y^{(i)})^2

所以线性回归模型，最终就是要找到这个θ，从而让MSE收敛至最小。

正规方程（The Normal Equation）

为了找到最小化代价函数的θ，其实有个方程可以直接给出答案，就是正规方程（The Normal Equation）

\hat{\theta}=(\mathrm{X}^\mathrm{T}\cdot\mathrm{X})^{-1}\cdot\mathrm{X}^\mathrm{T}\cdot\mathrm{y}

以下是证明过程，来自Deepseek。

\begin{aligned} J(\theta)&=(\mathrm{y}-\mathrm{X}\theta)^{T}(\mathrm{y}-\mathrm{X}\theta)\\ &=\mathrm{y}^{T}\mathrm{y}-\mathrm{y}^{T}\mathrm{X}\theta-\theta^{T}\mathrm{X}^{T}\mathrm{y}+\theta^{T}\mathrm{X}^{T}\mathrm{X}\theta\\ \quad\\ \mathrm{y}&:n\times 1\quad(n个观测值)\\ \mathrm{y}^{T}&:1\times n\quad(行向量)\\ \mathrm{X}&:n\times (p+1)\quad(n个观测值, p+1个特征)\\ \theta&:(p+1)\times 1\quad(列向量)\\ \mathrm{y}^{T}\mathrm{X}\theta&=1\times n \times n \times (p+1) \times (p+1) \times 1\\ &=1 \times 1\\ &=标量\\ &=\theta^{T}\mathrm{X}^{T}\mathrm{y}\\ \quad\\ J(\theta)&=\mathrm{y}^{T}\mathrm{y}-2\theta^{T}\mathrm{X}^{T}\mathrm{y}+\theta^{T}\mathrm{X}^{T}\mathrm{X}\theta\\ \quad\\ 对\theta求导数\\ \frac{\partial J(\theta)}{\partial \theta}&=\frac{\partial}{\partial \theta}(\mathrm{y}^{T}\mathrm{y}) - 2\frac{\partial}{\partial \theta}(\theta^{T}\mathrm{X}^{T}\mathrm{y})+\frac{\partial}{\partial \theta}(\theta^{T}\mathrm{X}^{T}\mathrm{X}\theta)\\ &=0-2\mathrm{X}^{T}\mathrm{y}+2\mathrm{X}^{T}\mathrm{X}\theta\\ \quad\\ 最小值处导数为0，所以\\ 0&=-2\mathrm{X}^{T}\mathrm{y}+2\mathrm{X}^{T}\mathrm{X}\theta\\ \mathrm{X}^{T}\mathrm{X}\theta&=\mathrm{X}^{T}\mathrm{y}\\ \theta&=(\mathrm{X}^{T}\mathrm{X})^{-1}\mathrm{X}^{T}\mathrm{y} \end{aligned}\\

再来看计算复杂度，X^TX，得到的是一个d*d的矩阵（这里的d指的是特征的数量），所以计算复杂度通常会达到O(d³)。所以当特征数量达到十万的量级时，计算就会非常耗时。

与y点积的时候，计算复杂度是O(n)，和训练集的数量呈正比，所以大的训练集也足以放入内存。

当训练好的模型用于预测时，仅仅是简单的X与θ的点积，与特征数呈正比，预测的复杂度并不高。

梯度下降（Gradient Descent）

梯度下降的定义

上文中的正规方程，虽然可以直接给出结果，但是仅适用于线性回归模型，且有较大的计算复杂度。还有一种算法，适用于多种模型，就是梯度下降（Gradient Descent）。

梯度，其实就是函数的导数。一元函数的导数表示这个函数图形的切线的斜率，多元函数上的梯度则是一个向量，它的方向是这个函数在某个点上最大增长的方向，它的量是在这个方向上的增长率。

梯度下降的目的，就是找到参数调整的方向，并最终找到整个代价函数的最低点，也就是梯度为0的点。参数调整的方向，就是梯度的反方向。

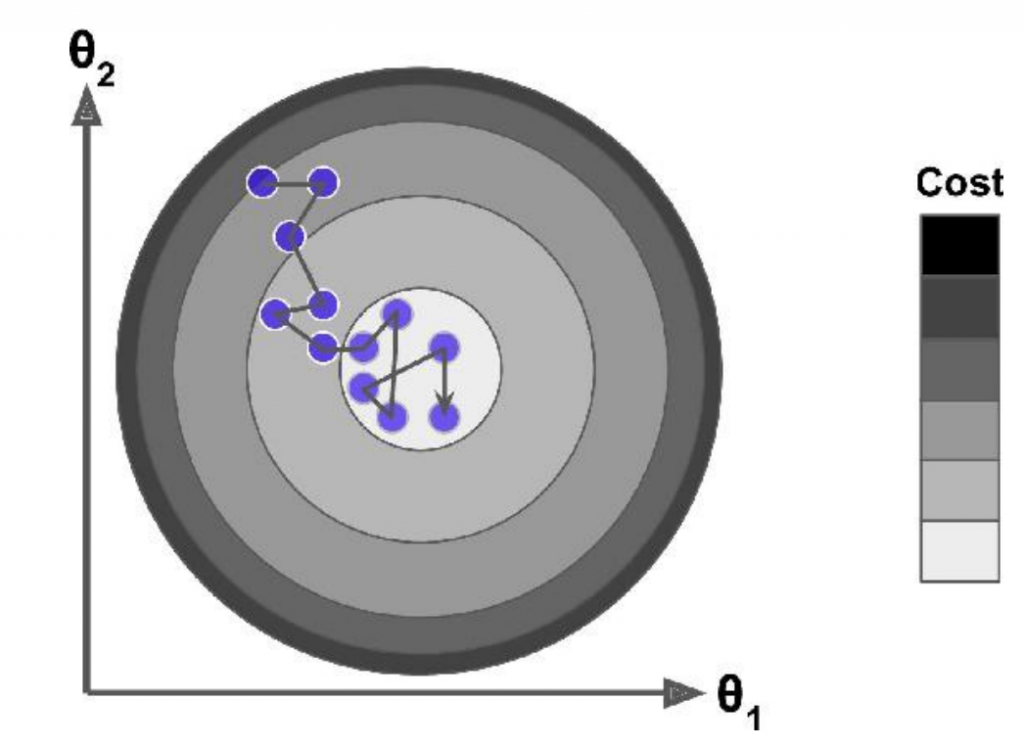
梯度下降的做法，就是先随机初始化一个起点（称为random initalization），不断迭代调整参数，并最终达到最优点，如下图所示：

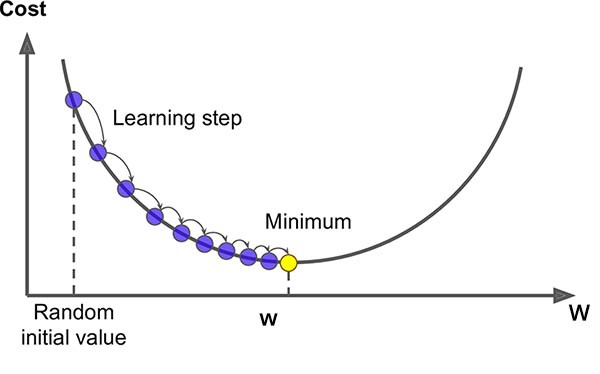
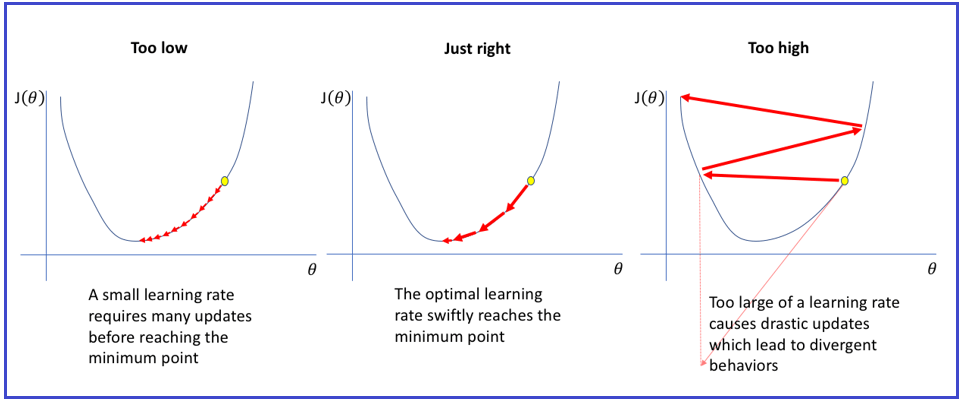
在调整过程中，比较重要的一个参数就是学习率（learning rate）。如果学习率太低，则会耗时太久才找到最优解；如果学习率过大，则会跳过最优解，而代价越来越大，导致训练失败。

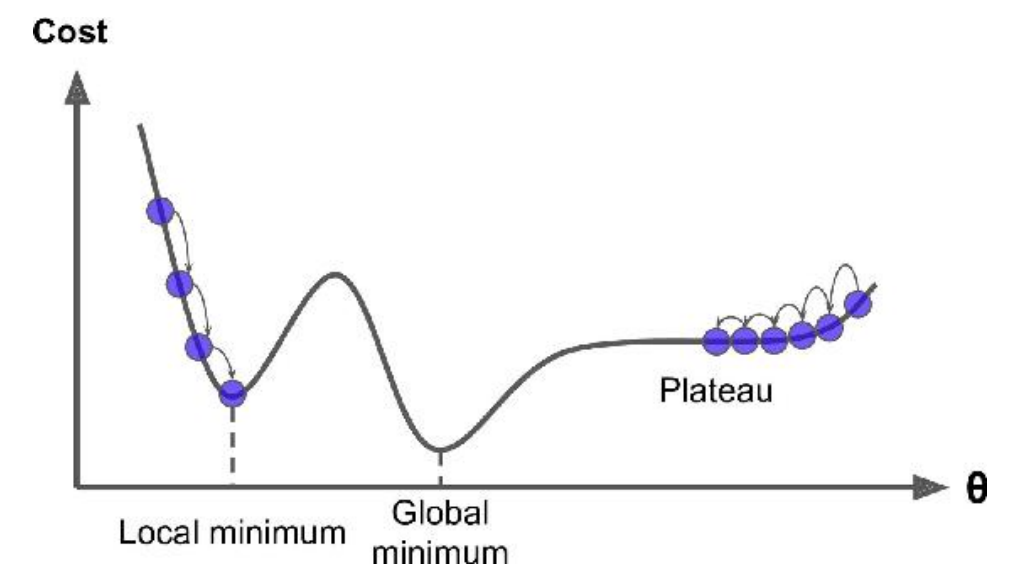
当然，并不是所有的代价函数都是完美的碗形状，实际可能有更多的复杂形状。如下图所示，如果起始点随机在左侧，则只会达到local最优（local minimum），并非全局最优（global minimum）。如果随机在右侧，则会耗费很久无法达到最优点。

然而对于线性回归模型来说，其代价函数是一个凸函数，所以肯定仅有一个全局最优点。因此只要学习率适当，等待足够的时间，最终肯定可以找到最优解。

线性回归模型的代价函数，是一个圆，但是如果不同特征之间的取值范围不一，则会变成椭圆，如下图所示

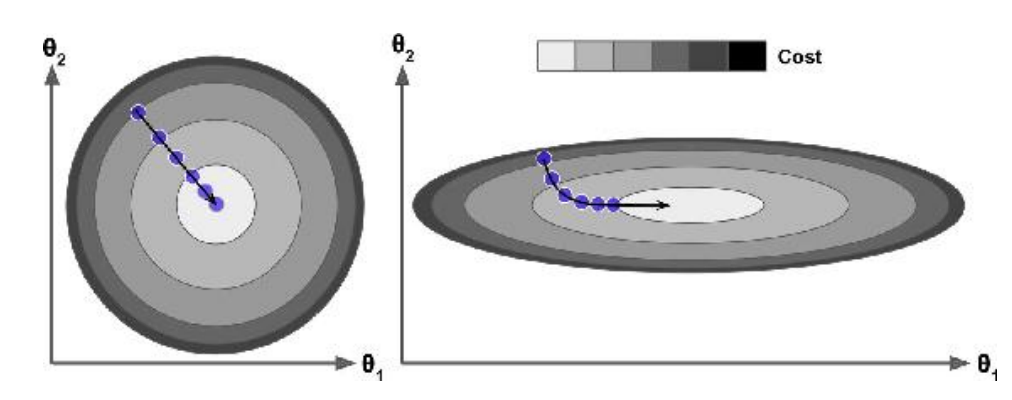
左边的图中，特征之间取值范围相同，则梯度下降的方向就是最优的方向，所以很快就能找到最优解。而右侧的图中，由于取值不相同，导致梯度下降的方向并非最优。所以在训练之间的准备过程中，就用通过Standard Scaler等手段，进行特征缩放，从而有利于更快找到最优解。

批量梯度下降（Batch Gradient Descent）

为了计算梯度下降，就需要计算出每个参数θ_j的梯度。换句话说，需要计算出θ_j变化后，代价函数会减少多少，称为偏导数（或者偏微分，partial derivative）。单个参数的偏导数公式以及推导过程如下：

\begin{aligned} J(\theta)&=\frac{1}{m}\sum_{i=1}^{m}(y^i-\hat{y^i})^2\\ \hat{y^i}&=\theta_0+\theta_1x_{i1}+\theta_2x_{i2}+...+\theta_px_{ip}=\sum_{j=0}^p\theta_jx_{ij}\\ \quad\\ 对特定参数\theta_j求偏导数\\ \frac{\partial{J}}{\partial{\theta_j}}&=\frac{\partial}{\partial{\theta_j}}\left[\frac{1}{m}\sum_{i=1}^{m}(y^i-\hat{y^i})^2\right]\\ &=\frac{1}{m}\sum_{i=1}^{m}\frac{\partial}{\partial{\theta_j}}\left[(y^i-\hat{y^i})^2\right]\\ \quad\\ \frac{\partial}{\partial{\theta_j}}\left[(y^i-\hat{y^i})^2\right]&=2(y^i-\hat{y^i})\frac{\partial}{\partial{\theta_j}}(y^i-\hat{y^i})\\ \quad\\ 由于y_i为常数，不依赖\theta_j\\ \frac{\partial}{\partial{\theta_j}}(y^i-\hat{y^i}) &=-\frac{\partial\hat{y^i}}{\partial\theta_j}\\ \quad\\ 非\theta_j的项都视为常数\\ \frac{\partial\hat{y^i}}{\partial\theta_j}&=x_{ij}\\ \quad\\ 组合起来后就有\\ \frac{\partial{J}}{\partial{\theta_j}}&=\frac{2}{m}\sum_{i=1}^{m}(\hat{y^i}-y^i)x_{ij} \end{aligned}

梯度向量，记为▽_θMSE(θ)，包含了每一个参数的偏导数方程，如下所示

\nabla_{\theta}MSE(\theta)=\left( \begin{aligned} \frac{\partial}{\partial\theta_0}MSE(\theta)\\ \frac{\partial}{\partial\theta_1}MSE(\theta)\\ ...\\ \frac{\partial}{\partial\theta_n}MSE(\theta)\\ \end{aligned} \right)=\frac{2}{m}\mathrm{X}^{T}\cdot(\mathrm{X}\cdot\theta-\mathrm{y})

这里的计算复杂度为O(nd)，其中n为样本数，d为特征数。这里每一步迭代，都会使用全部的样本数进行训练，所以对于大训练集来说还是很耗时的。不过相比于正规方程（The Normal Equation）来说，海量特征的场景下，梯度下降的优势还是比较明显的。

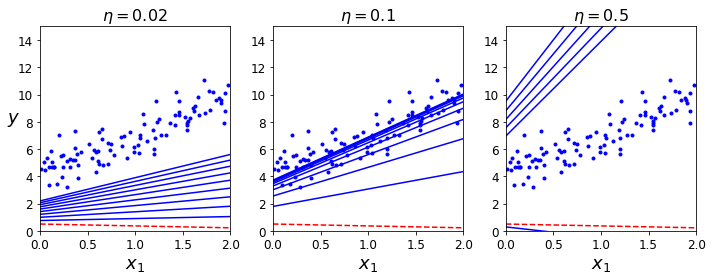
每次迭代需要调整参数，这里引入了学习率 η，每次调整都会乘上学习率。

\theta^{(next\ step)}=\theta-\eta\nabla_{\theta}MSE(\theta)

不同的学习率的效果如下图所示。学习率太低的时候，迭代了很多次仍然没有达到最优。学习率太高的时候，会直接错过最优解。只有学习率合适的时候，才能在有效的迭代中找到最优解。

随机梯度下降（Stochastic Gradient Descent）

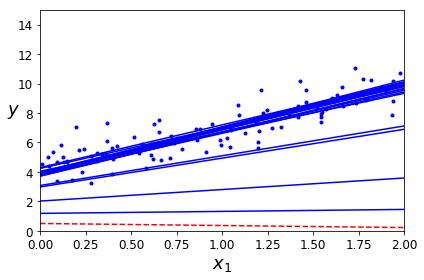
批量梯度下降的问题，就是每一次迭代都需要完整的训练集进行计算，计算成本太高。所以SGD每一步迭代的时候，仅挑选一个样本进行梯度计算，如下所示。所以即使是大的训练集，每一步迭代的速度也会很快。

\nabla_{\theta}MSE(\theta)=2x_i^{T}\cdot(x_i\cdot\theta-y_i)

另一方面，SGD由于随机的特性，当达到临近最优解的时候，并不会收敛，而是会在最优解附近反复，如下图所示。所以SGD算法终止的时候，结果是临近最优，但并不一定是最优。

SGD还有一点好处，就是随机特性，所以有可能能跳过local最优，而达到全局最优。

如下图所示，经过10次迭代后，最终也是可以找到最优附近的解。

小批量梯度下降（Mini-batch Gradient Descent）

既然SGD太多随机，批量的方式计算量太大，那么就选择一种中间的方式，就是挑选样本的时候，仅随机挑选小批量的样本进行学习。

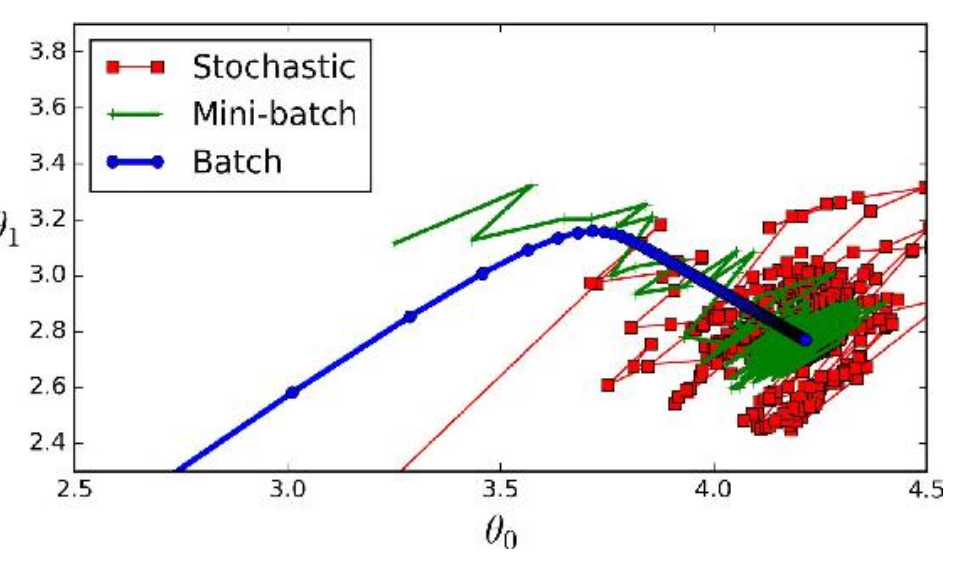
如下图所示，使用三种方式进行训练。batch方式会持续迭代到最优解，而SGD和mini-batch两种都会在最优解附近反复横跳。相比而言，mini-batch的幅度更小，不会偏离太多。

下表就是三种方式的一个对比，m为样本数，n为特征数。

算法	Large m	Out-of-core support	Large n	Scaling required
正规方程	Fast	No	Slow	No
批量梯度下降	Slow	No	Fast	Yes
随机梯度下降	Fast	Yes	Fast	Yes
小批量梯度下降	Fast	Yes	Fast	Yes

多项式回归（Polynomial Regression）

多项式回归的实现

比如有一个多项式模型为y=ax²+bx+c，多项式会自动发现特征的多项式关系。对于这个例子，之前的单一特征{x}，就会被拓展为{x, x²}两个特征。根据这两个特征再去进行线性回归，从而找到对应的参数。

多项式展开，就是根据多项式的最高项数，穷举所有的可能。比如有两个特征a和b，最高项数为3，则多项式展开后，会增加a²,b²,a³,b³,ab,a²b,ab²。

多项式展开的公式，就是最高项数d，n个特征，最终会展开出(n+d)! / d!n! 个特征。

这个问题其实就是d个项数，需要分到n个特征上，每个特征上可以为0。

\begin{aligned} e_1+e_2+e_3+...+e_n&\leqslant d, \quad e_i\geqslant0\\ 引入辅助变量e_{n+1} &= d-(e_1+e_2+e_3+...+e_n)\\ e_1+e_2+e_3+...+e_n+e_{n+1}&=d\\ 等价于d个球放入n+1个盒子，&盒子可空\\ 等价于d+n+1个球放入n+1个盒子，&盒子不可空\\ 根据隔板法，可得：\\ \left(\frac{d+n}{n}\right)&=\frac{(d+n)!}{d!n!} \end{aligned}

学习曲线（Learning Curve）

毫无疑问，当多项式的项数更高的时候，就能与训练模型更拟合，如下图所示：

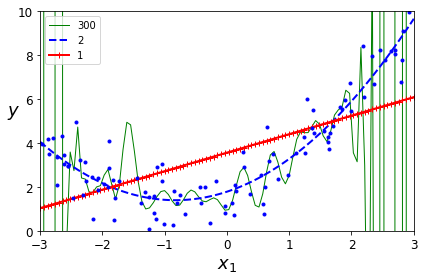
从上图可以看到，线性模型明显是欠拟合，而300项的多项式模型则明显过拟合。那么如何判断一个模型是欠拟合还是过拟合呢？这就需要引入学习曲线（Learning Curve）来进行判断。

上图中的数据用线性模型来拟合，其学习曲线如下图所示，曲线上的两条线分别是训练集和验证集的表现。

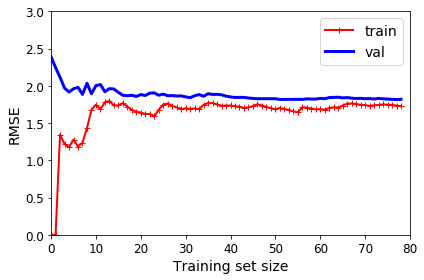
当训练集很少的时候，比如仅有1-2个样本，则线性模型很容易拟合训练集，代价基本为0。但是这个模型明显无法拟合验证模型，初始代价很很大。

随着训练集样本数增加，线性模型无法完美拟合了，代价也随之增加，随后样本数再增加也无法改善了。而在验证集上的表现，样本数增加也能帮忙模型更好拟合验证集，但后续后续无法继续改善了。

这个图就是明显的欠拟合，模型过于简单，以至于样本数增加也无法继续优化。

再用最高10项的多项式模型来拟合同样的数据，其学习曲线如下图所示：

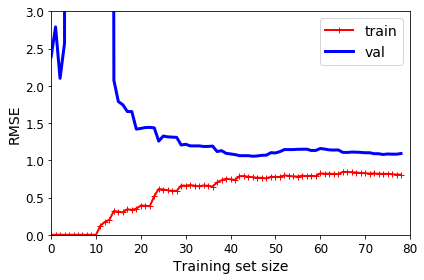
通过这张图可以看出，相比于线性模型，代价明显更小。但是同样可以看到，训练集的表现要比验证集的表现要好，当然这也是过拟合的表现。随着样本数增加，两者之间的差距也会渐渐缩小。

Bias/Variance Tradeoff

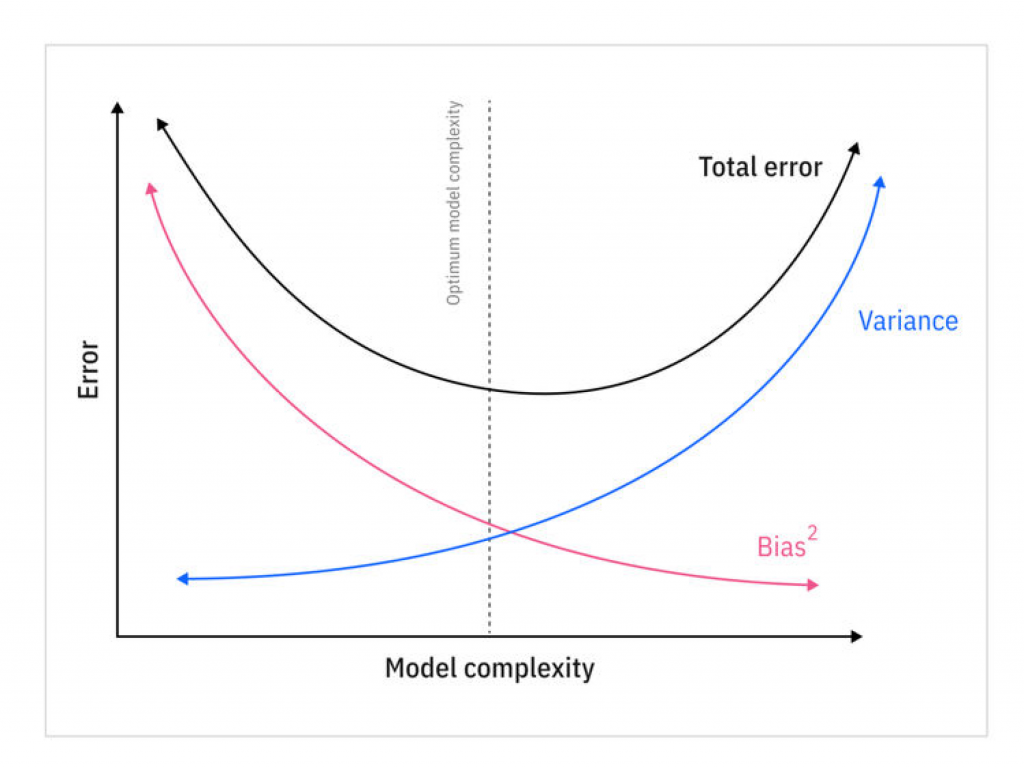
一个模型的泛化误差，可以表达为三部分误差之和：

Bias。这部分的误差，主要是因为模型的预测与真实值之间的差异。可能是选择了错误的模型，比如多项式场景用了线性模型。如果这部分误差很大，则代表模型是欠拟合的。
Variance。这部分的误差，主要是因为模型对于训练集中的一些小的偏差过于敏感，甚至尽量去拟合训练集中的正常噪音，从而导致不同的验证集会有不同的表现，也就是过拟合。
Irreducible error。一般是由于训练集中的噪音导致，这种需要数据清理来减少噪音的影响。

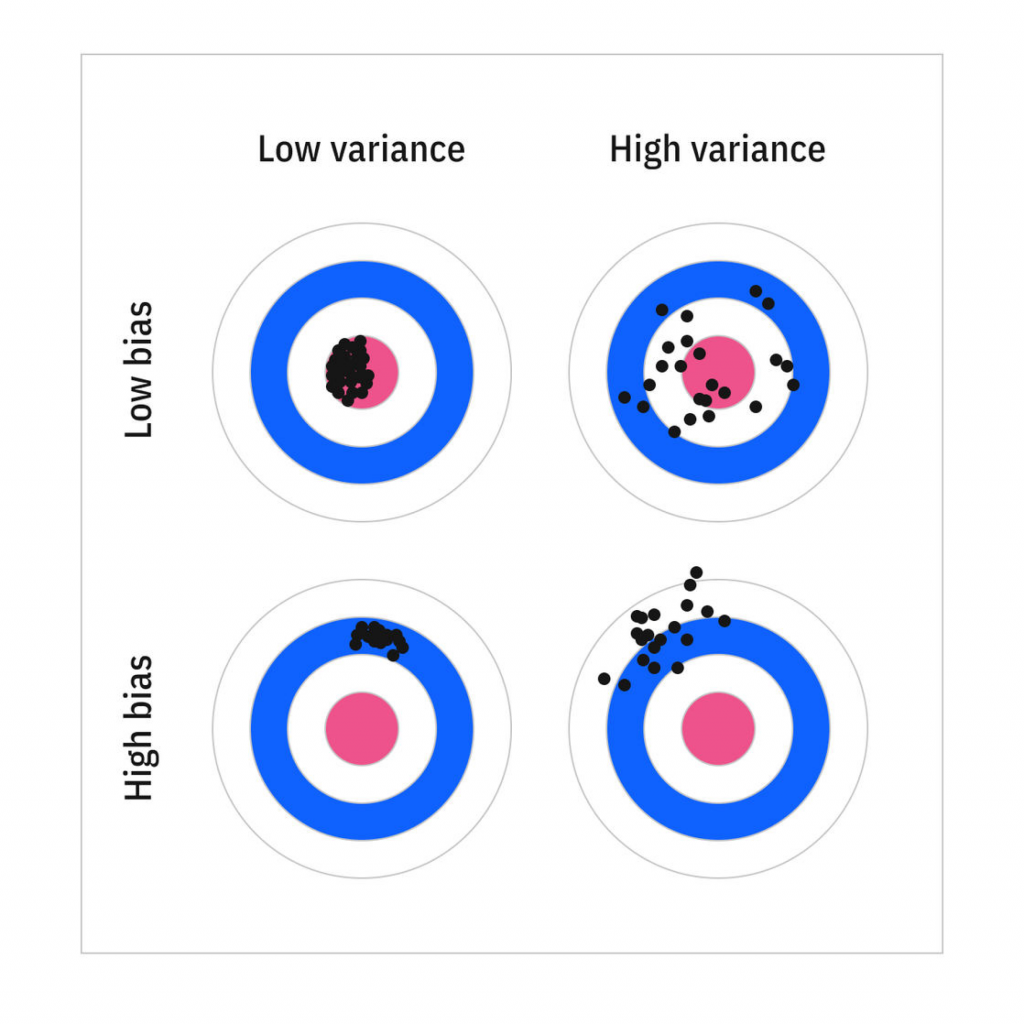
所以提升模型的复杂度，就会增加variance，而减少bias。相反，减少模型的复杂度，会增加bias，减少variance。具体如下图所示：

正则化的线性模型（Regularized Linear Models）

第一章提到，为了避免过拟合，可以通过正则化来限制模型的复杂度。对于线性模型来说，正则化有三种方式：Ridge Regression，Lasso Regression，Elastic Net。

Ridge Regression

Ridge Regression（也称Tikhonov正则化）是正则化版本的线性回归。具体做法就是在代价函数中增加特征权重的l₂-norm，这就保证拟合模型不会有太大的权重。

超参数α用于设置正则化的程度，如果为0，则没有任何的限制，等价于线性回归。如果很大，则权重会被限制到基本为0，那么模型就退化为一个常量（样本的平均值）了。

正则化后的代价函数，可以描述为

J(\theta)=MSE(\theta)+\alpha\frac{1}{2}\sum_{i=1}^{n}\theta_i^2

因为是平方求和，所以参数权重的归一化特别重要，不要有太大的值，否则会被放大而影响结果。

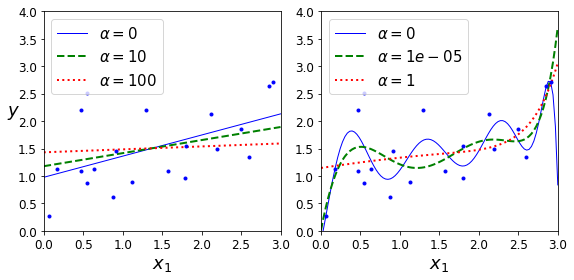
下图就是不同超参数对于模型的限制效果。左侧的线性回归，α为0时为原始的模型，α越大，模型斜率越低。右侧的多项式回归模型，α越大，模型越平缓，波动越小。

Ridge Regression求解

Ridge Regression也有直接求解的方程，这里的A是一个n*n的单位矩阵。

\hat\theta=\left(\mathrm{X}^T\cdot\mathrm{X} + \alpha\mathrm{A}\right)^{-1}\cdot\mathrm{X}^T\cdot\mathrm{y}

证明过程如下

\begin{aligned} J(\theta)&=(\mathrm{y}-\mathrm{X}\theta)^{T}(\mathrm{y}-\mathrm{X}\theta)+\alpha\theta^T\theta\\ &=\mathrm{y}^{T}\mathrm{y}-\mathrm{y}^{T}\mathrm{X}\theta-\theta^{T}\mathrm{X}^{T}\mathrm{y}+\theta^{T}\mathrm{X}^{T}\mathrm{X}\theta+\alpha\theta^T\theta\\ &=\mathrm{y}^{T}\mathrm{y}-2\theta^{T}\mathrm{X}^{T}\mathrm{y}+\theta^{T}\mathrm{X}^{T}\mathrm{X}\theta+\alpha\theta^T\theta\\ \quad\\ 对\theta求导数\\ \frac{\partial J(\theta)}{\partial \theta}&=\frac{\partial}{\partial \theta}(\mathrm{y}^{T}\mathrm{y}) - 2\frac{\partial}{\partial \theta}(\theta^{T}\mathrm{X}^{T}\mathrm{y})+\frac{\partial}{\partial \theta}(\theta^{T}\mathrm{X}^{T}\mathrm{X}\theta)+\frac{\partial}{\partial \theta}(\alpha\theta^T\theta)\\ &=0-2\mathrm{X}^{T}\mathrm{y}+2\mathrm{X}^{T}\mathrm{X}\theta+2\alpha\theta\\ \quad\\ 最小值处导数为&0，所以\\ \mathrm{X}^{T}\mathrm{X}\theta+\alpha\theta&=\mathrm{X}^{T}\mathrm{y}\\ 为了对齐\mathrm{X}^{T}\mathrm{X}，&需要乘以单位矩阵\\ (\mathrm{X}^{T}\mathrm{X}+\alpha\mathrm{A})\theta&=\mathrm{X}^{T}\mathrm{y}\\ \theta&=(\mathrm{X}^{T}\mathrm{X}+\alpha\mathrm{A})^{-1}\mathrm{X}^{T}\mathrm{y} \end{aligned}\\

Lasso Regression

Lasso Regression，使用的是l₁-norm，其公式如下

J(\theta)=MSE(\theta)+\alpha\sum_{i=1}^{n}|\theta_i|

下图就是Lasso Regression对于模型的约束效果

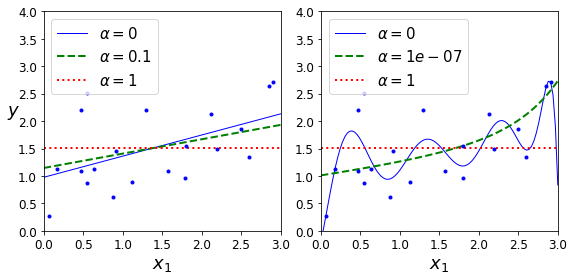
对于Ridge和Lasso两张图可以发现一个明显的不同点。同样的最大约束条件下，Ridge左侧线性模型的斜率接近0，但还是会稍微大于0，右侧多项式模型仍然为多项式。而相比之下，Lasso左侧的线性模型斜率直接为0，左侧多项式模型也退化为斜率为0的直线，也就是说参数被限制为0了。

这就是Lasso Regression的一个关键特性，就是它可以将不重要的特征参数直接降为0，从而实现了特征选择的效果，最终会输出一个稀疏的模型（仅保留重要特征参数）。

为什么Ridge Regression只能让参数接近0，而Lasso Regression可以让参数降为0呢？可以从下图中得出答案

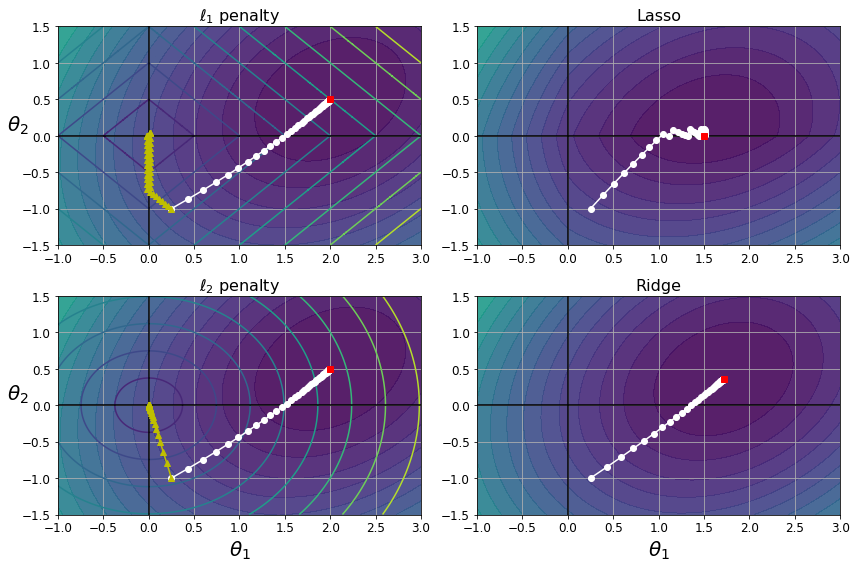
左上图中，椭圆是未正则化的代价函数（仅有两个参数θ₁和θ₂），每一圈的代价相同（代价函数的等高线）。白色点连成的线，就是通过BGD（批量梯度下降）寻找最优解的路径。

菱形则是l₁-norm的代价约束（不同参数绝对值相加，因此是一个菱形，l₂-norm是一个椭圆）。黄色点的连接，就是BGD寻找α->∞时的最优解，路径基本是沿着代价等高线的垂直方向，先定位到θ₁的点，再定位到θ₁和θ₂都是0的点。

因此，正则化后的线性模型，本质就是寻找在一定的约束条件下（l₁-norm的菱形范围内，l₂-norm的椭圆范围内），求出代价函数的最小值。l₁-norm限制下，椭圆与菱形的切点，很大概率是菱形的顶点，因此就会将某些参数限制为0。

右上的图，就是α=0.5情况下正则化的代价函数，其等高线不是标准的椭圆了，左侧有一个突出的尖角，因为左侧有一个l₁-norm的额外代价，越靠左额外代价越小。最终的最优解将θ₂限制为0了。

而下面两张图则是Ridge Regression。首先椭圆与椭圆的切点，不太会出现在参数为0的坐标轴上，因此最后的最优解也是θ₂接近0。

Lasso Regression求解

Lasso Regression没有closed-form solution，不过也有办法求解，其证明过程如下：

\begin{aligned} J(\theta)&=MSE(\theta)+\alpha\sum_{j=0}^p|\theta_j|\\ \frac{\partial J(\theta)}{\partial \theta_j}&=\frac{2}{m}\sum_{i=1}^{m}(\hat{y^i}-y^i)x_{ij} + \alpha\frac{\partial|\theta_j|}{\partial{\theta_j}}\\ 由于\theta_j为0处&不可微分，求\theta_j的次梯度\\ \frac{\partial|\theta_j|}{\partial{\theta_j}}&=sign(\theta_j)\\ \quad\\ 因此\\ g(\theta,J)&=\nabla_{\theta}MSE(\theta)+\alpha\left( \begin{aligned} sign(\theta_1)\\ sign(\theta_2)\\ ...\\ sign(\theta_n)\\ \end{aligned} \right) \quad\\ \end{aligned}

Elastic Net

Elastic Net是结合Ridge Regression和Lasso Regression的一种正则化方式，并通过一个参数r来控制更偏向于哪一种正则化方式。其公式如下

J(\theta)=MSE(\theta)+r\alpha\sum_{i=1}^n|\theta_j|+\frac{1-r}{2}\alpha\sum_{i=1}^n\theta_i^2

r是介于0～1的参数，当r=0时等价于Ridge Regression，当r=1时等价于Lasso Regression。实际情况中，一般会更偏向于Lasso Regression，因为可以去除掉无用的特征。

早停法（Early Stopping）

为了避免过拟合，还有一种办法就是使用早停法（Early Stopping），也就是说当验证误差低于阈值后，及时终止训练，从而避免过拟合。

下图就是通过BGD训练一个高阶多项式模型的学习曲线，可以看出随着训练次数越来越多，虽然训练的误差越来越小，但是在验证集的误差却渐渐增加，表示这个模型已经开始过拟合了。

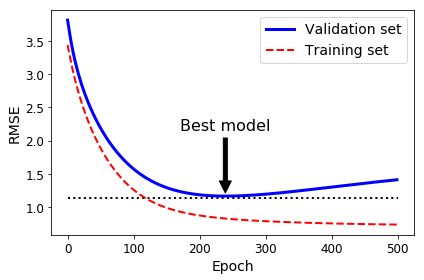
对于随机梯度下降或者小批量梯度下降，学习曲线并不一定如上图那般平滑，所以并不好判断何时应该及时停止。一个有效的判断办法，就是当误差持续停留在最小值附近，则可以断定模型已经无法继续优化了，将参数回滚到最小值那一步即可。

逻辑回归（Logistic Regression）

在第一章提到，有些回归算法也可以用于分类。逻辑回归就是用于预测一个样本属于某个分类的概率（比如这个邮件是垃圾邮件的概率），概率大于等于50%则判断属于该分类（positive，标记为1），否则不属于该分类（negtive，标记为0），因此也是一个二元分类器。

预测概率

逻辑回归和线性回归类似，也是需要输入特征以及特征的参数（权重），不同的是它仅输出一个概率，其向量化方式表达如下：

\hat{p}=h_{\theta}(\mathrm{x})=\sigma(\theta^T\cdot \mathrm{x})

σ是一个sigmoid函数，呈S型，其具体公式以及图形表达如下所示

\sigma(t)=\frac{1}{1+e^{-t}}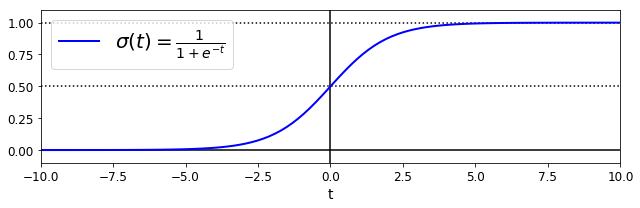

当计算出概率后，最终的分类结果通过下式可以得出：

\hat{y}=\begin{cases} 0\quad if\ \hat{p}\ <\ 0.5,\\ 1\quad if\ \hat{p}\ \ge\ 0.5. \end{cases}

训练模型及代价函数

那么应该如何训练一个逻辑回归模型呢？训练的目的就是找到这样的参数，能让y=1的样本预测概率很高（接近1），并让y=0的样本预测概率很低（接近0）。因此如果模型的预测概率恰好与之相反，就要给予较大的惩罚，让其概率特别大。因此单个样本的代价函数可以定位为：

c(\theta)=\begin{cases} -log(\hat{p}) \qquad &if\ y=1,\\ -log(1-\hat{p}) &if\ y=0.\\ \end{cases}

当y=1且概率接近0时，会返回特别大的值，同样当y=0且概率接近1的时候，也会返回大数。因此实现了预测不符合预期给予较大代价的目的。

总体的代价函数，就是所有样本代价的平均值，如下式所示：

J(\theta)=-\frac{1}{m}\sum_{i=1}^m\left[y^{(i)}log(\hat{p}^{(i)}) + (1-y^{(i)})log(1-\hat{p}^{(i)})\right]

这里的代价函数，没有一个类似正规方程那样的求解，不过可以针对某一个参数求偏导数，从而利用梯度下降算法来寻求最优解。某一参数的偏导数推导过程如下：

\begin{aligned} 首先，&log函数的导数为\\ log'(p) &= \frac{1}{p}\\ sigmoid&函数的导数为\\ \sigma'(z)&=\sigma(z)(1-\sigma(z))\\ 逻辑回归&输出的导数为（BGD部分有类似过程）\\ \frac{\partial}{\partial\theta_j}(\theta^T\cdot\mathrm{x})&=x_{ij}\\ \quad\\ 因此&应用链式法则\\ \frac{\partial}{\partial{\theta_j}}J(\theta)&=-\frac{1}{m}\sum_{i=1}^{m}\frac{\partial}{\partial{\theta_j}}\left[y^{(i)}log(\hat{p}^{(i)}) + (1-y^{(i)})log(1-\hat{p}^{(i)}))\right]\\ &=-\frac{1}{m}\sum_{i=1}^{m}\left[\frac{y^{(i)}}{\sigma^{(i)}} + \frac{1-y^{(i)}}{1-\sigma^{(i)}}\right]\cdot\left[\sigma^{(i)}(1-\sigma^{(i)})\right]\cdot x_{ij}\\ &=-\frac{1}{m}\sum_{i=1}^{m}(\sigma(\theta^T\cdot\mathrm{x}^{(i)})-y^{(i)})x_{ij} \end{aligned}

Softmax Regression

逻辑回归也可以用于多分类场景，不需要像第三章那样训练多个二元分类器。这种多分类场景，也被称为Softmax Rgression或者多元逻辑回归（Multinomial Logistic Regression）。

其原理也是比较简单易懂，对于一个样本x，回归模型会针对每个分类k计算一个得分s_k(x)，然后通过softmax函数来预估每个分类的概率。

计算每个分类k得分的方法，与线性回归算法类似，具体如下

s_k(\mathrm{x})=\theta_k^T\cdot\mathrm{x}

每一个分类都有其独有的参数向量θ_k，每个向量都是参数矩阵Θ的一行。

计算概率时使用的softmax函数，定义如下所示

\hat{p_k}=\sigma(\mathrm{s}(\mathrm{x}))_k=\frac{\exp(s_k(\mathrm{x}))}{\sum_{j=1}^{K}\exp(s_j(\mathrm{x}))}

K为分类的数量
s(x)是某个样本x在每个分类得分的向量
σ(s(x))_k是样本x属于某个分类的概率

与逻辑回归分类器类似，最终也是根据概率高低，找到最终属于的分类。

\hat{y}=\argmax_k\ \sigma(\mathrm{s}(\mathrm{x}))_k=\argmax_k\ s_k(\mathrm{x})=\argmax_k\ (\theta_k^T\cdot\mathrm{x})

那么模型训练时的代价函数，目标就是对于某个样本，其正确的分类有最高的概率，其他分类都概率很低。这种代价函数，也被称为交叉熵（cross entropy）。当y为1，但是概率很低的时候，其代价就会很大，从而用来惩罚预测错误的模型。

J(\Theta)=-\frac{1}{m}\sum_{i=1}^m\sum_{k=1}^K y_k^{(i)}\log(\hat{p}_k^{(i)})

对于某个分类k，其梯度向量如下所示

\nabla_{\theta_k}J(\Theta)=\frac{1}{m}\sum_{i=1}^m(\hat{p}_k^{(i)}-y_k^{(i)})\mathrm{x}^{(i)}