RNN和CNN序列处理数据
循环神经网络(Recurrent Neural Networks)
RNN可以分析时间序列数据,例如你网站的每日活跃用户数、城市的每小时温度、家庭的日用电量、附近车辆的行驶轨迹等等。一旦RNN学会了数据中过去的模式,它就能运用其知识来预测未来。
更广泛地说,RNN能够处理任意长度的序列,而非固定尺寸的输入。例如,它们可以将句子、文档或音频样本作为输入,这使其在自然语言处理应用中极为有用,例如自动翻译或语音转文字。
循环神经元(Recurrent Neurons)
一个最简单的RNN,只包含一个神经元。神经元接受输入,产生输出,又将输出发给自己,如下图所示。

当随着时间的推移,每个时间点的输入就是x(i)和y(i-1),而第一个时刻没有之前的输出,因此默认为0。这种方式就是按时间展开(unrolling the network through time)。
一个循环神经元的输出,可以表示为
\hat{\bold{y}}(t)=\varphi(\bold{W}_{x}^{T}\bold{x}_{(t)} + \bold{W}_{\hat{y}}^{T}\bold{\hat{y}}_{(t-1)}+\bold{b})- ϕ为激活函数(比如ReLU)
- b为偏置向量
- x(t)为t时刻的输入
- y(t)为t时刻的输出
- W为两种输入的权重
记忆单元(Memory Cells)
既然神经元可以接受之前时刻的输出作为输入参数,那么可以认为神经元具有记忆功能。一个简单的循环神经元,一般都可以学习到短暂的记忆。
记忆单元在某一时刻的记忆,可以标记为h(t),它是当前输入与前一步骤记忆的函数,h(t)=f(x(t), h(t-1))。
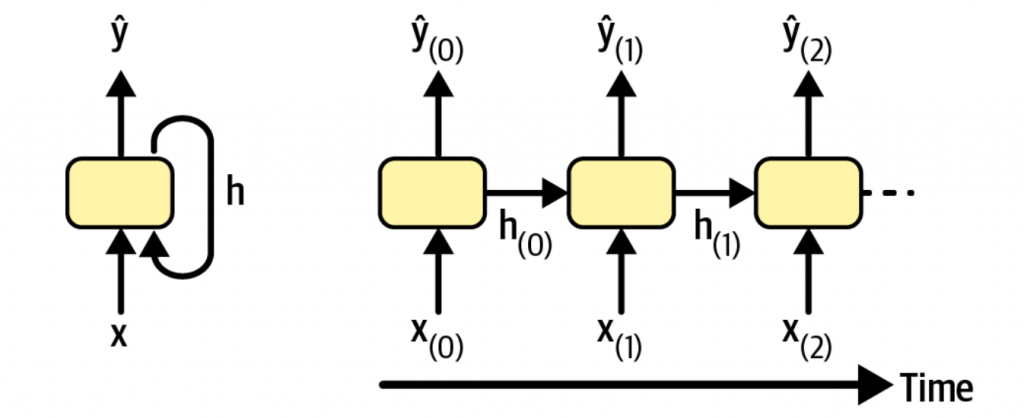
RNN的输入与输出
sequence-to-sequence
主要用于时间预测场景,比如根据过去的电力消耗,来预测未来一段时间的电力消耗。
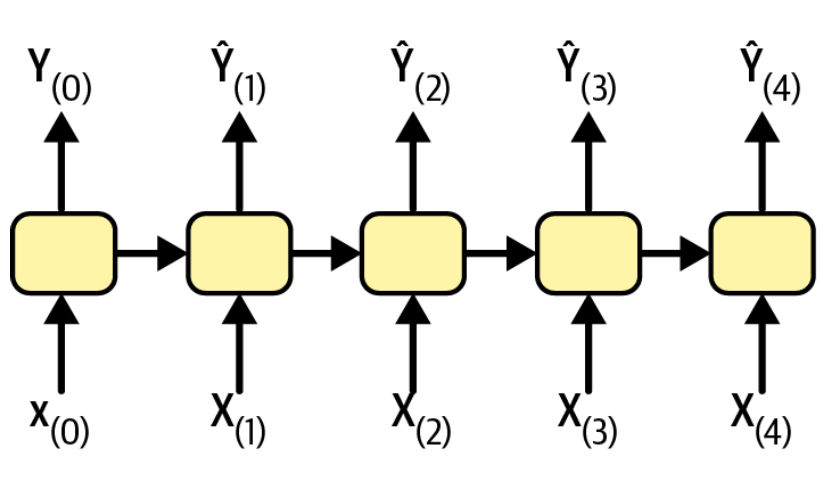
sequence-to-vector
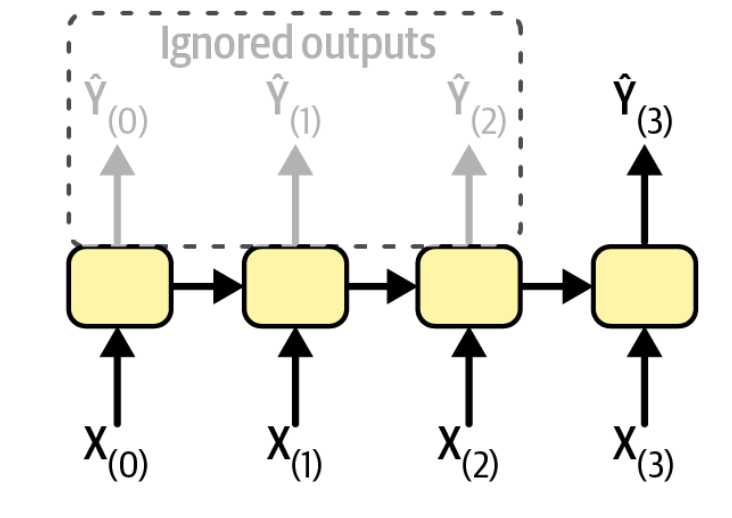
输入一段序列后,忽略之前步骤的输出,仅关注最后一步的输出。比如输入一段影评,最终输出这段影评的情感得分。
vector-to-sequence
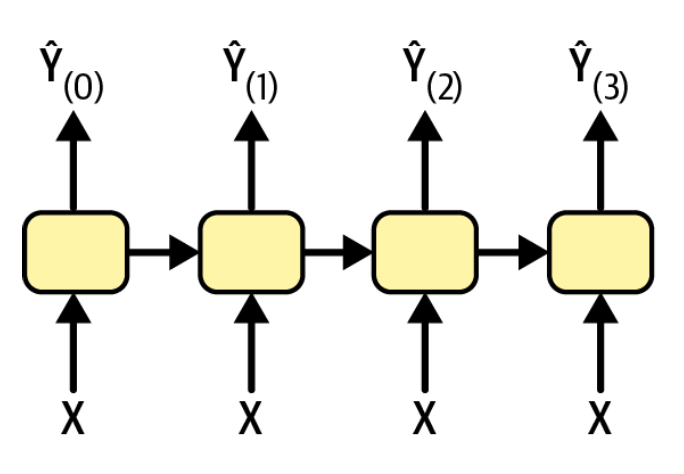
也可以每一个步骤都输入相同的输入,但是产出一系列的输出。比如输入一张图片,产出图片的摘要信息。
encoder-decoder
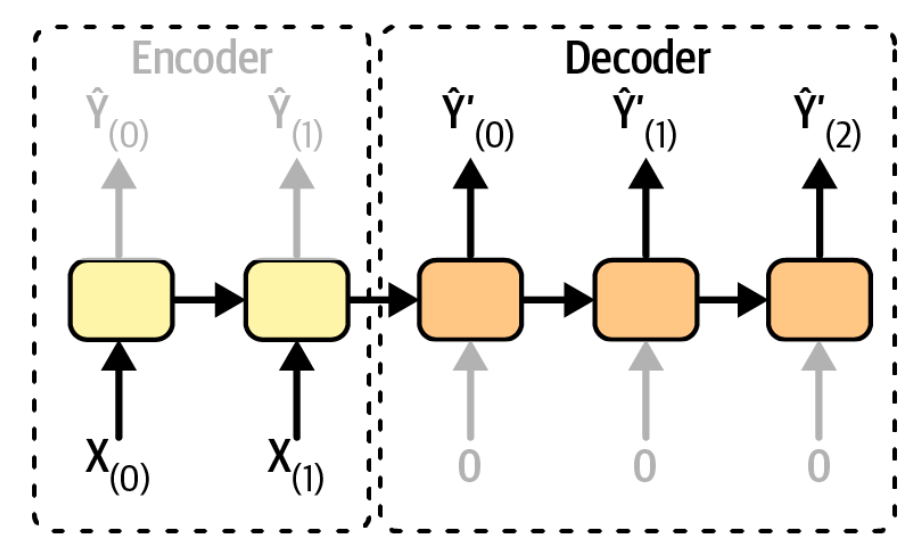
先有一个sequence-to-vector的网络,称为encoder,再接着一个vector-to-sequence的网络,称为decoder。比如翻译的场景,必须等待完整的句子输入后,才能进行翻译并逐词输出。
长期记忆(Long-term Memory)
传统的RNN在处理长序列时,信息在每一步都会经过变换和传递。在反向传播过程中,梯度需要跨越许多时间步进行连乘,极易导致梯度消失或梯度爆炸,从而使网络无法学习到远距离信息之间的关联。因此,需要用长期记忆单元,来解决此类问题。
LSTM(Long Short-Term Memory)
一个LSTM单元的结构,如下图所示。其最大的不同,就是将记忆分为了两种:
- 短期记忆,h(t)
- 长期记忆,c(t)
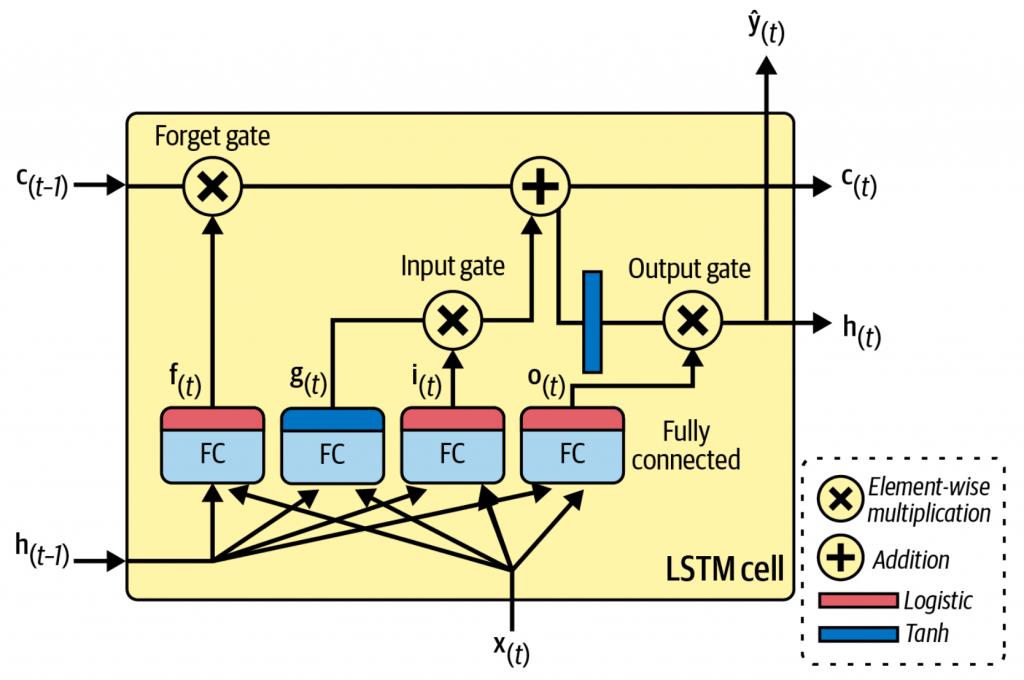
LSTM的核心,就是三个门与一个单元状态。三个门都是逻辑激活函数,输出范围0-1。而输出会紧跟着逐项相乘操作,所以输出0就会关闭门,输出1则彻底打开门。
- g(t),通过分析输入x(t)以及上个步骤的短期记忆h(t-1),来更新单元的状态。在LSTM中,输出并没有直接给出去,而是会将最重要的部分存入长期记忆。
- f(t),遗忘门。用来控制哪些长期记忆需要被移除
- i(t),输入门。用来控制g(t)的哪些信息需要存入长期记忆
- o(t),输出门。用来控制长期记忆中的哪些信息需要输出到h(t)和y(t)
其具体的计算公式如下
\begin{align*}
\bold{i}_{(t)}&=\sigma({\bold{W}_{xi}}^T\bold{x}_{(t)} + {\bold{W}_{hi}}^T\bold{h}_{(t-1)} + \bold{b}_i) \\
\bold{f}_{(t)}&=\sigma({\bold{W}_{xf}}^T\bold{x}_{(t)} + {\bold{W}_{hf}}^T\bold{h}_{(t-1)} + \bold{b}_f) \\
\bold{o}_{(t)}&=\sigma({\bold{W}_{xo}}^T\bold{x}_{(t)} + {\bold{W}_{ho}}^T\bold{h}_{(t-1)} + \bold{b}_o) \\
\bold{g}_{(t)}&=\text{tanh}({\bold{W}_{xg}}^T\bold{x}_{(t)} + {\bold{W}_{hg}}^T\bold{h}_{(t-1)} + \bold{b}_g) \\
\bold{c}_{(t)}&= \bold{f}_{(t)}\otimes\bold{c}_{(t-1)} + \bold{i}_{(t)}\otimes\bold{g}_{(t)}\\
\bold{y}_{(t)}&=\bold{h}_{(t)}=\bold{o}_{(t)}\otimes\text{tanh}(\bold{c}_{(t)})
\end{align*}门控循环单元(GRU)
与拥有三个门(遗忘、输入、输出)和一个独立单元状态的LSTM不同,GRU(gated recurrent unit)通过更精简的设计达到了相似的目标。
其结构图如下图所示
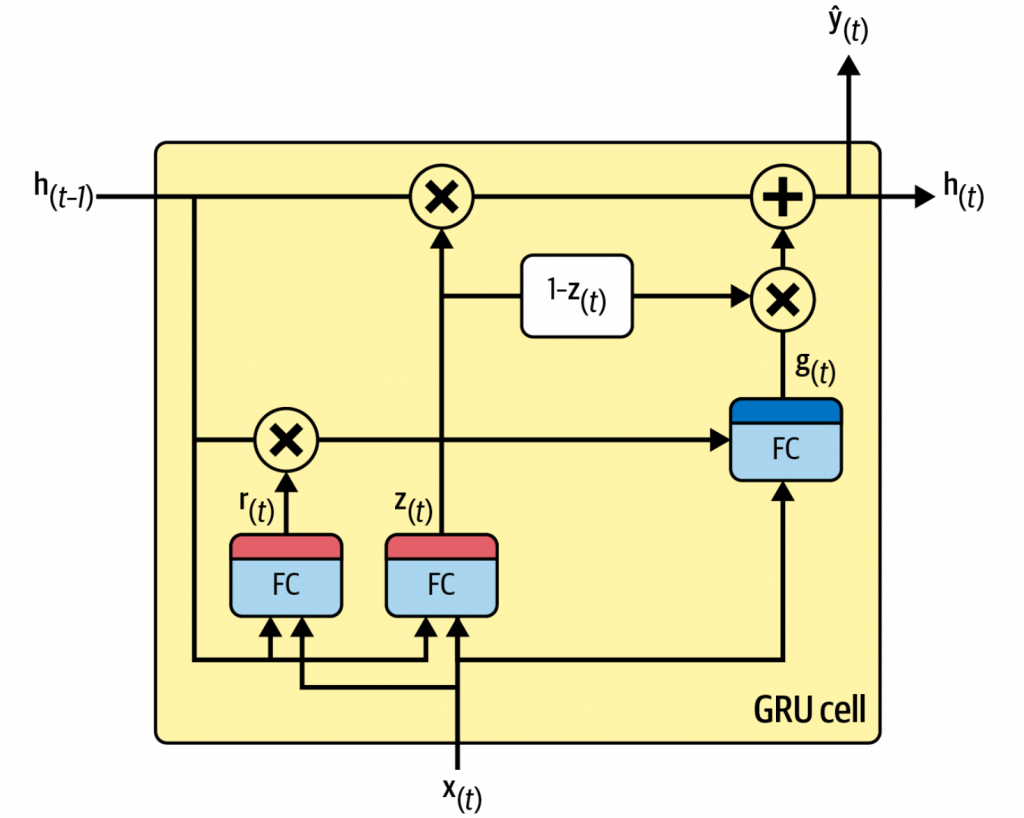
GRU可以说是LSTM的简化版本,主要做了以下几种简化
- 不再区分两种状态,都合并到同一个h(t)中
- 新的更新门z(t),它直接决定了有多少旧信息被保留,以及有多少新信息被加入。它同时扮演了LSTM中“遗忘门”和“输入门”的角色。更新门输出1时,输入门关闭,遗忘门打开。输出0时,输入门打开,遗忘门关闭。
- 新的重置门r(t),控制在计算新的候选状态时,应忽略多少过去的隐藏状态信息。它决定了过去的记忆如何与当前输入结合以生成新的想法。
GRU的具体计算公式为:
\begin{align*}
\bold{z}_{(t)}&=\sigma({\bold{W}_{xz}}^T\bold{x}_{(t)} + {\bold{W}_{hz}}^T\bold{h}_{(t-1)} + \bold{b}_z) \\
\bold{r}_{(t)}&=\sigma({\bold{W}_{xr}}^T\bold{x}_{(t)} + {\bold{W}_{hr}}^T\bold{h}_{(t-1)} + \bold{b}_r) \\
\bold{g}_{(t)}&=\text{tanh}({\bold{W}_{xg}}^T\bold{x}_{(t)} + {\bold{W}_{hg}}^T(\bold{r}_{(t)}\otimes\bold{h}_{(t-1)}) + \bold{b}_g) \\
\bold{h}_{(t)}&=\bold{z}_{(t)}\otimes\bold{h}_{(t-1)} + (1-\bold{z}_{(t)})\otimes\bold{g}_{(t)}
\end{align*}