训练深度神经网络
梯度消失/爆炸
反向传播算法,从输出层传递到输入层,计算w和b的梯度,从而对这些参数进行微调。
如果在传递过程中,梯度逐渐减少,到输入层时参数更新的幅度很小,导致无法收敛,称之为梯度消失(vanishing gradient)。而某些情况则恰恰相反,梯度在传递过程中逐渐变大,导致最后的参数更新幅度很大,模型也会远远偏离目标,称为梯度爆炸(exploding gradient)。
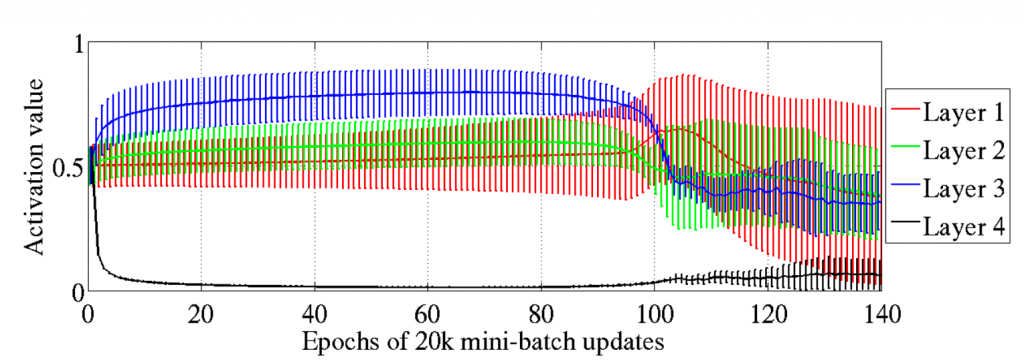
2010年的一篇论文《Understanding the Difficulty of Training Deep Feedforward Neural Network》,证明了之前的深度神经网络,采用Sigmoid函数以及权重初始化技巧(均值为0,[-1/√n, 1/√n]均匀分布),会导致在从底层向顶层传播的过程中,其方差逐层递减。这导致所有层的激活值分布都逐渐变得“狭窄”,信息容量下降。另外,第四层的激活值早早达到了饱和区,导致后续反向传播的时候,梯度基本为0,其他层就更没有太多的梯度可以调整了。如下图所示:
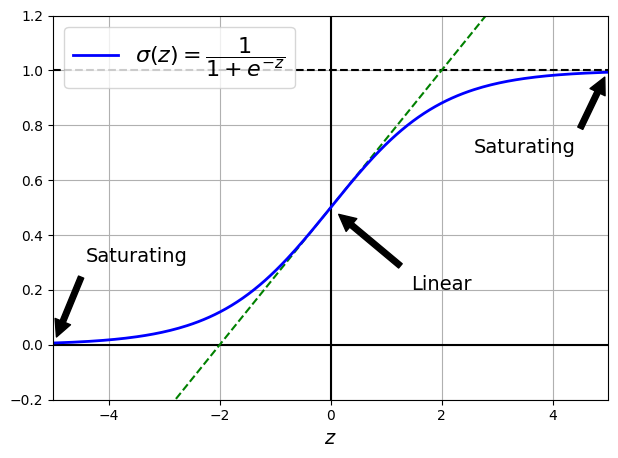
Sigmoid函数如下图所示,当接近极值0或者1的时候,导数接近0,就是饱和区了。
权重初始化优化
论文中还发现,如果要保持信号量能够正常传递下去,没有梯度消失或者爆炸的问题,就需要保证每层的输入方差与输出的方差相等。但是每一层的输入和输出神经元数量可能不等(称为fan-in和fan-out),论文就提出了取均值,fanavg = (fanin + fanout) / 2)。那么如何让每一层的输入与输出方差相等呢?其初始化方式,根据论文的作者命名,称为Xavier初始化 或者 Glorot初始化。具体推导如下
对于一个在区间 [a, b] 上服从均匀分布的随机变量 X,其方差计算公式为:
Var(X)=\frac{(b-a)^2}{12}因此,为了达到保持每一层的输入输出方差相等,需要满足这样的均匀分布
W \sim U[-r, +r]\\
r=\sqrt{\frac{3}{\text{fan}_{avg}}}或者这样的正态分布
W \sim N(0,\frac{1}{\text{fan}_{avg}})LeCun提出的初始化方式很类似
W \sim N(0,\frac{1}{\text{fan}_{in}})此外,还有He初始化
W \sim N(0,\frac{2}{\text{fan}_{in}})激活函数优化
ReLU激活函数虽然计算简单,但是实际中会存在神经元“坏死”的问题。只要输入小于0,那么其输出肯定为0,梯度下降也无法进行下去了。
Leaky ReLU
其激活函数定义为LeakyReLUα(z) = max(αz, z),α就是z<0时的变化斜率。这样就保证了z<0时的梯度不为0,后续参数还可以继续调整。
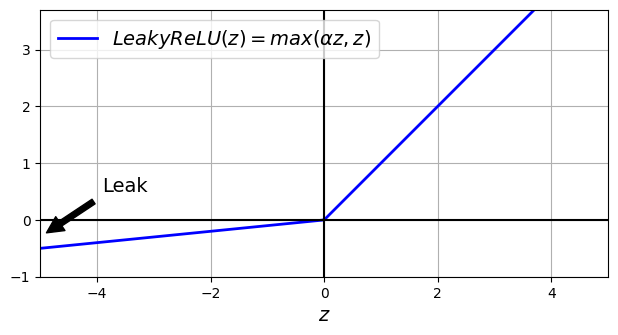
但是和ReLU存在同样的问题,就是非平滑曲线,z=0处不可导。这就会导致梯度下降在最优处左右震荡,从而让整个模型无法收敛。
ELU
ELU(exponential linear unit)是一个平滑的曲线,其定义如下
\text{ELU}_{\alpha}(z)=
\begin{cases}
\alpha(\exp(z)-1) & \text{if } z \lt 0 \\
z & \text{if } z \ge 0
\end{cases}- z<0时取值负数,这样总体均值接近0,从而减轻梯度消失的问题
- z<0时的梯度不为0,这样避免了神经元坏死的问题
- 当α=1时,整体为为平滑的曲线,z=0时导数为1,避免了最优解附近无法收敛的问题
此外,后续有人提出了SELU(scaled ELU),其定义为
\text{SELU}(z)=1.05 \text{ ELU}_{1.67}(z)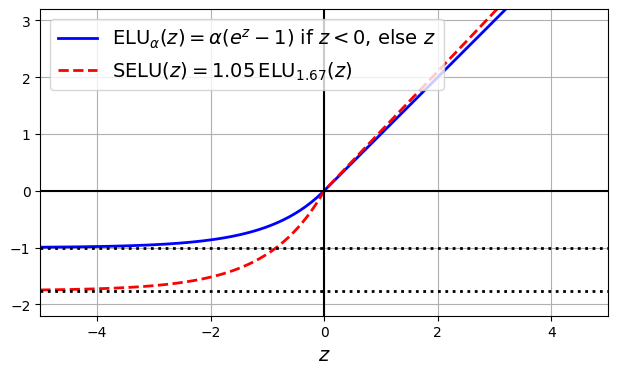
GELU
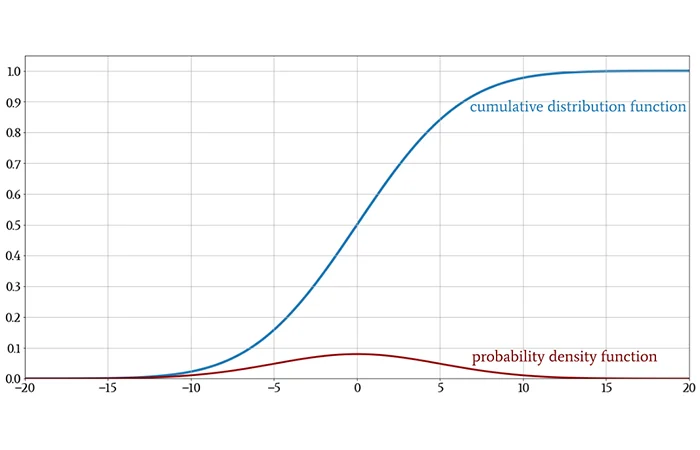
GELU同样时ReLU的一种平滑方式,它是基于高斯累积分布函数(Gaussian cumulative distribution function)来定义的,记为Φ。Φ(z)指的就是在一个均值为0方差为1的正态分布中,小于z的概率。
\Phi(z)=\frac{1}{2\pi}\int_{\infty}^z e^{-\frac{x^2}{2}}dx其变化曲线如下图所示
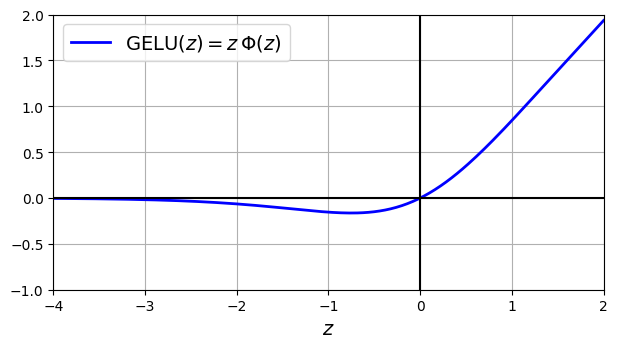
GELU的定义以及曲线如下所示
\text{GELU}(z)=z\Phi(z)- z趋向负无穷,激活值接近0;z趋向正无穷,激活值接近z
- 之前的激活函数都基本是凸函数,而该激活函数的变化曲线比较复杂,从而能够模拟更复杂的场景
- 计算成本较高
Swish
GELU的计算较为耗时,因此后续有人提出了Swish激活函数,当参数为1.75时,其曲线与GELU很接近,但是计算成本要少很多
\text{Swish}_\beta(z)=z\sigma(\beta z)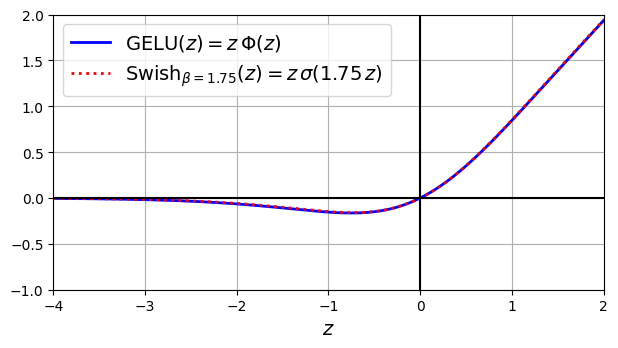
批量归一化(Batch Normalization)
批量归一化,就是在每个隐藏层的激活函数之前,增加了归一化的操作,也就是使其强制转化为均值为0、方差为1的标准分布,然后通过两个参数分别来进行缩放(scale)和偏移(shift)。其具体的算法如下:
\begin{align*}
\mu_B&=\frac{1}{m_B}\sum_{i=1}^{m_B}\bold{x}^{(i)} \\
\quad\\
{\sigma_B}^2 &= \frac{1}{m_B}\sum_{i=1}^{m_B}(\bold{x}^{(i)} - \mu_B)^2\\
\quad\\
{\hat{\bold{x}}}^{(i)} &= \frac{\bold{x}^{(i)} - \mu_B}{\sqrt{{\sigma_B}^2 + \varepsilon}}\\
\quad\\
{\bold{z}}^{(i)} &= \gamma \otimes {\hat{\bold{x}}}^{(i)} + \beta
\end{align*}- μB为输入样本的一次批次B的均值矩阵
- mB为这批次的样本数
- σB为这批次样本的标准差
- x(i)为经过归一化后的第i个样本
- ε是为了避免除0,也被称为平滑项(smoothing term)
- γ为该层输出的缩放向量,每个样本有一个缩放值
- ⊗代表逐项相乘
- β为该层输出的偏移向量,每个样本有一个偏移量
- z(i)为经过缩放和偏移后的输出
这两个参数(通常记为 γ 和 β)的作用是:让网络能够自行学习,决定在多大程度上保留或改变由BN强制带来的标准化分布。正是由于这两个可学习参数的存在,批量归一化才能做到既稳定了训练过程,又丝毫不损害网络的非线性表达能力,甚至在很多情况下还能增强它。
但是,BN增加了模型的复杂度,此外在预测的时候也会有明显的额外代价。
梯度裁剪(Gradient Clipping)
为了避免梯度爆炸,从而导致的模型不稳定问题,我们就需要限制梯度的值,比如使用梯度裁剪(Gradient Clipping)。梯度裁剪的核心思想非常简单直接:当模型参数的梯度向量过大时,我们将其“裁剪”或“缩小”,使其模长不超过一个我们设定的阈值。其主要作用有:
- 稳定训练过程:使训练过程更加平滑、可预测,尤其是在训练难以驯服的模型(如RNN、Transformer)时。
- 防止训练不稳定:有效解决梯度爆炸问题,避免损失值剧烈震荡。
- 允许使用更高的学习率:因为梯度大小被限制,即使学习率稍高,参数的更新步长也不会过大,这有时能加快收敛速度。
一种是按值裁剪,将值限制在某个范围内,比如[-clip_value, +clip_value]。但是这样可能会导致梯度的方向发生改变。比如[0.9, 100]方向会紧贴Y轴,但是裁剪后的值[0.9, 1.0],其方向基本就是双轴之间的对角线了。
另一种方式就是按范数裁剪,从而让梯度向量的方向不变。比如之前的[0.9, 100],裁剪后的向量为[0.00899964, 0.9999595]。
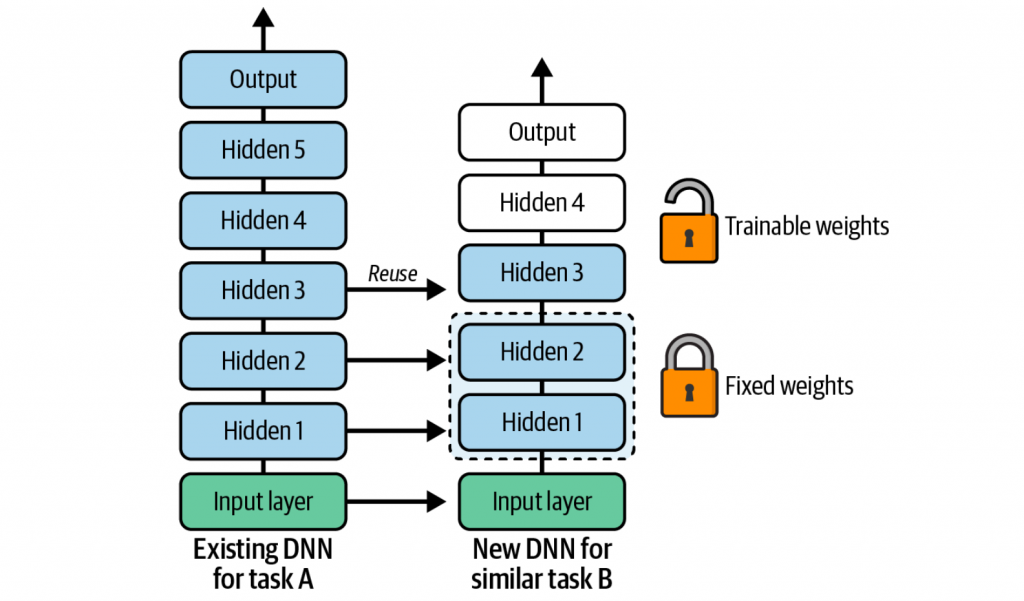
复用预训练层
如果存在另一个已经训练好的神经网络,其训练任务比较类似,那么就可以从这个神经网络中复用靠近底层的一些隐藏层。而靠近输出的那些隐藏层,由于训练目标不同,基本是无法复用的。
这种复用其他神经网络的训练方式,也被称为迁移学习(transfer learning),具体工作流程如下图所示
无监督预训练(Unsupervised pretraining)
相对来说,未打标的数据比打标数据更容易获取到。因此,可以拿这些未打标数据进行无监督的预训练,选用一些无监督模型(比如autoencoder,GAN等)。这样的话,底层的一些隐藏层就可以拿到复用,再加上一些其他层,再来训练监督模型。如下图所示
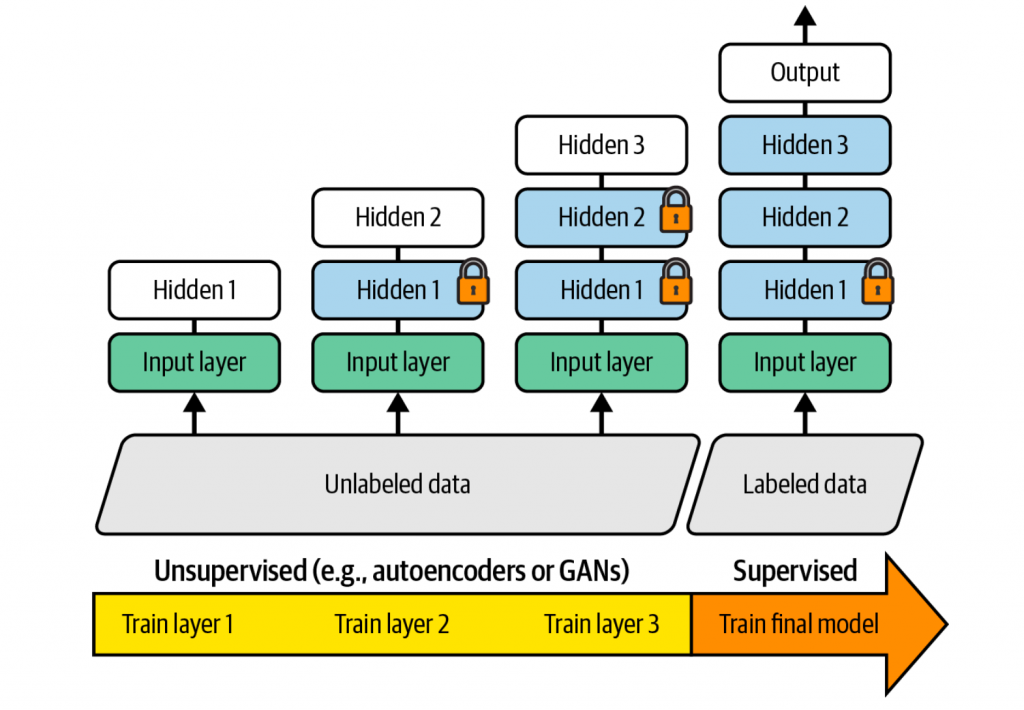
举例来说,原先的目标是人脸识别,需要大量的打标数据(标注到人的具体图片)。而现在可以先通过一堆未打标的人脸图片,进行无监督的预训练,其底层的输出肯定会包含人脸的一些基本特征,比如性别、肤色等。这些特征完全是可以在后续的监督学习中复用的。
更快的优化器
除了梯度下降,还有很多其他的优化器可以选择。
动量法(Momentum)
常规的梯度下降,根据斜率来调整参数,斜率越大调整幅度越大,但是不会累积这个幅度。而动量法的原理就是要加速梯度下降的过程。就像一个小球顺着斜坡滚下去,其速度会逐渐增大,直到空气阻力或者摩擦力等作用下达到最大值。
其公式如下:
\begin{align*}
\bold{m} &\gets \beta\bold{m} - \eta \nabla_\theta J(\theta) \\
\theta &\gets \theta + \bold{m}
\end{align*}- θ为权重向量
- ∇θJ(θ)为权重调整的梯度
- η为学习率
- m为动量向量(momentum vector),会累积之前所有的梯度
- β为动量系数,起到了摩擦力的作用,防止持续增长
当m到达极值时,差不多为1/(1-β)个梯度。比如β=0.9时,就会有10倍的放大。
动量法类似于一个滚下山坡的球,当球遇到一个小洼地(局部最小值)时,由于惯性(即积累的动量),它不会立即停止,而是继续向前滚动。在优化中,即使当前梯度很小(接近零),m仍然包含之前梯度的方向和信息,因此参数更新不会在局部最小值处完全停止,从而有可能跳过局部最小值。
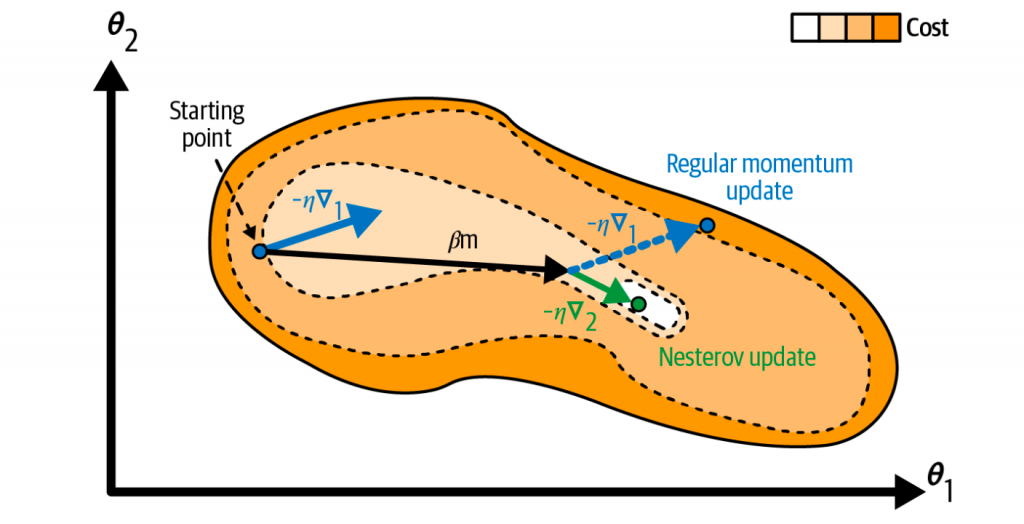
Nesterov 加速梯度(Nesterov Accelerated Gradient)
Nesterov加速梯度(NAG),针对动量法的一处计算做了优化,就是并没有计算θ处的梯度,而是下一步将要达到处的梯度,如下式所示
\begin{align*}
\bold{m} &\gets \beta\bold{m} - \eta \nabla_\theta J(\theta + \beta\bold{m}) \\
\theta &\gets \theta + \bold{m}
\end{align*}首先,它根据累积的动量进行一次临时更新,先“跳”到未来一个大概的位置。然后,在这个“未来”的位置计算梯度。最后,用这个“未来”的梯度来修正最初的动量更新。
这样做的好处,一方面会让梯度更新更加准确,如下图所示。
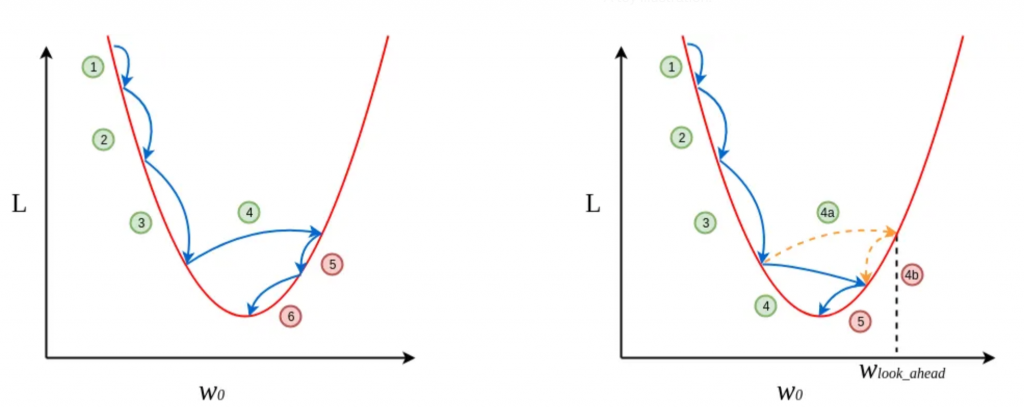
另一方面,在损失函数曲面弯曲程度较高时,能有效减少震荡,从而加速收敛,如下图所示。由于提前看到了梯度发生的变化,因此第四步的更新幅度就是减少。
自适应梯度(AdaGrad)
之前第四章提到遇到特征未缩放,代价函数会呈椭圆,导致梯度下降的方向并未朝着最优方向。而自适应梯度算法,则可自动为每个参数适应不同的学习率,其公式如下
\begin{align*}
\bold{s} &\gets \bold{s} + \nabla_\theta J(\theta) \otimes \nabla_\theta J(\theta) \\
\theta & \gets \theta - \eta \nabla_\theta J(\theta) \oslash \sqrt{\bold{s}+\epsilon}
\end{align*}- s为梯度平方的累积值
- ⊘代表逐项相除
- ε为平滑项,防止除0
在更新参数时,使用一个全局学习率除以这个累积量的平方根。这意味着:
- 对于频繁更新、梯度较大的参数,其累积值会很大,从而导致有效的学习率变小。
- 对于不频繁更新、梯度较小的参数,其累积值会很小,从而有效的学习率相对较大。
效果就是如下图所示,陡峭的维度会减少更新,从而让梯度更新方向更朝着最优方向。
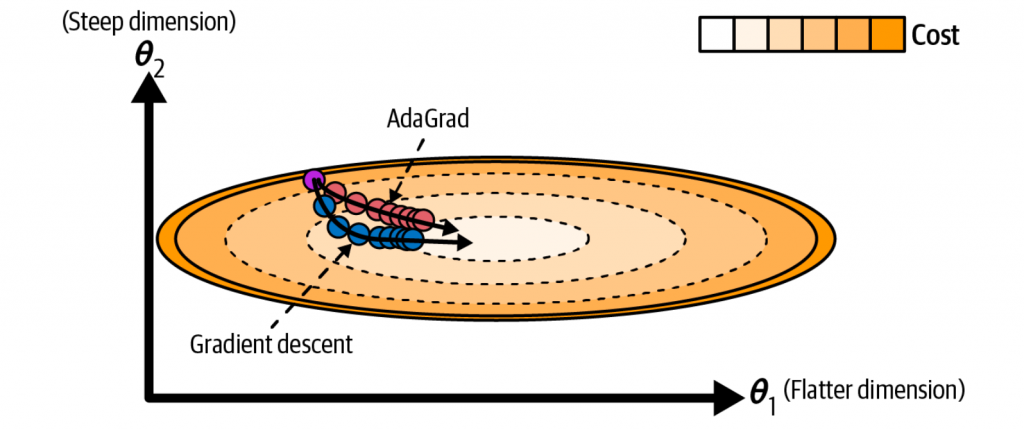
然后缺点比较明显,s在整个训练过程中只增不减,导致学习率会持续单调下降,最终变得无限小,以至于在训练后期参数可能完全停止更新。
均方根传播(RMSProp)
RMSProp(Root Mean Square Propagation)算法,是针对AdaGrad的改进,旨在解决 AdaGrad 学习率单调递减至零的问题。
\begin{align*}
\bold{s} &\gets \rho\bold{s} + (1-\rho)\nabla_\theta J(\theta) \otimes \nabla_\theta J(\theta) \\
\theta & \gets \theta - \eta \nabla_\theta J(\theta) \oslash \sqrt{\bold{s}+\epsilon}
\end{align*}- ρ为衰减参数,默认为0.9
RMSProp 使用指数衰减的移动平均来累积历史梯度,这意味着它更关注最近的梯度信息。通过衰减系数,使得历史平方梯度的累积量不会无限增长,从而避免了学习率持续下降的问题。
自适应矩估计(Adam)
Adam(adaptive moment estimation),它结合了之前两种优化算法的核心思想:动量法 和 RMSProp,并进行了改进,被认为是当前深度学习领域最通用、最有效的优化算法之一。
\begin{align*}
\bold{m} &\gets \beta_1\bold{m} - (1-\beta_1) \nabla_\theta J(\theta) \tag{1}\\
\bold{s} &\gets \beta_2\bold{s} + (1-\beta_2)\nabla_\theta J(\theta) \otimes \nabla_\theta J(\theta) \tag{2}\\
\widehat{\bold{m}} &\gets \frac{\bold{m}}{1-{\beta_1}^T} \tag{3}\\
\hat{\bold{s}} &\gets \frac{\bold{s}}{1-{\beta_2}^T} \tag{4}\\
\theta &\gets \theta - \eta \bold{m} \oslash \sqrt{\bold{s} + \epsilon} \tag{5}
\end{align*}- 式1,使用指数加权移动平均来估计梯度的均值(方向),这类似于动量法,帮助加速收敛并减少振荡。为梯度的一阶矩(first moment)。
- 式2,使用指数加权移动平均来估计梯度平方的均值(尺度),这类似于RMSProp,用于为每个参数自适应调整学习率。为梯度的二阶矩(second moment)。
- 式3和4,因为初始值都是0,因此通过偏差校正,避免初始值都在0附近。
- 式5,使用校正过的一阶矩和二阶矩来更新参数
Adam 因其卓越的性能和易用性,已成为深度学习领域事实上的标准优化器。
此外还有相关的三个变种算法,AdaMax,Nadam 和 AdamW。
AdamW(Adam with Decoupled Weight Decay)
在标准的Adam中,正则化一般是通过L2正则化来实现的,就是在代价函数中增加特征权重的l2-norm。这样计算出的梯度中就会加上权重衰减项
g_t=\nabla_\theta J(\theta) + \lambda\theta
但是这也带来了一个问题,上段的式5,自适应调整学习率,也会减少权重衰减的效果,从而起不到正则化的作用了。而AdamW将权重衰减解耦出来单独计算,因此最后一步就变成了
\theta \gets \theta - \eta (\bold{m} \oslash \sqrt{\bold{s} + \epsilon} + \lambda\theta)学习率的调度
学习率的选择非常重要。如果设置过大,训练过程就会发散。而设置过小,虽然最终能找到最优解,但是会耗时很久。而设置一个比较大的值,虽然训练初期进展会很大,但最终会在最优解附近震荡。
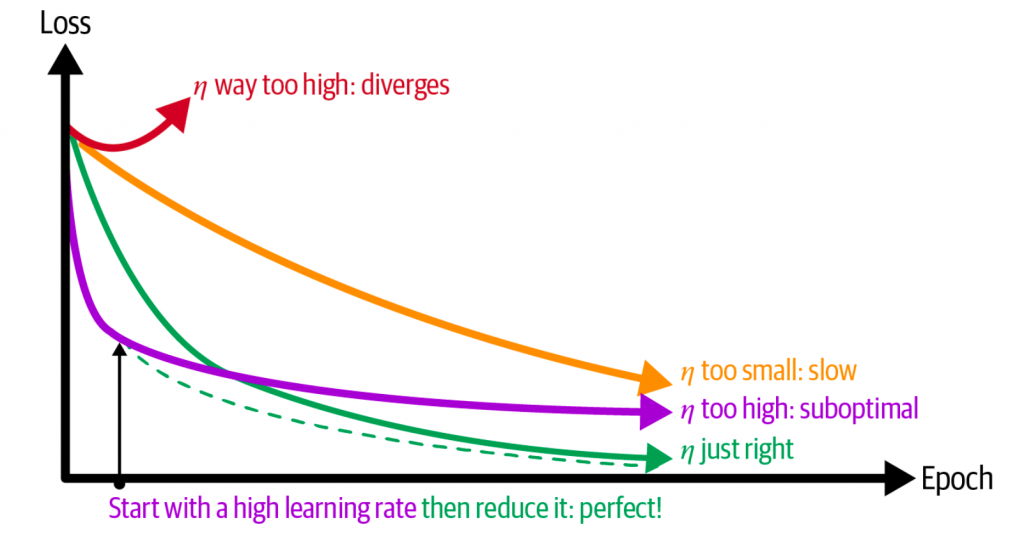
最好的做法,就是先用一个比较高的学习率,加快训练进度,再适时调整为较小的学习率。学习率的调度有以下几种。
幂调度(Power scheduling)
\eta(t)=\frac{\eta_0}{(1+t/s)^c}- t为迭代次数
- η0为初始的学习率
- s为步长参数,代表学习率多久衰减一次
- c为幂指数,通常设置为1
指数调度(Exponential scheduling)
\eta(t)=\eta_0 0.1^{t/s}- 每次衰减的幅度更大,直接降为之前的1/10
分段常数调度(Piecewise constant scheduling)
\begin{align*}
\eta_0=0.1 && \text{for 5 epochs} \\
\eta_0=0.01 && \text{for 50 epochs} \\
\dots
\end{align*}性能自适应调度(Performance scheduling)
每N步就计算下验证误差,当模型在验证集上的性能停止提升时,将学习率乘上系数λ进行衰减。
单周期调度(1cycle scheduling)
- 前半段,学习率线性增加至一个比较大的值
- 后半段,学习率线性降低至一个较小的值
- 单周期调度一般和动量结合使用,动量的选择刚好相反,前半段减少后半段增加
正则化
随机失活(Dropout)
核心思想:
训练过程的每次迭代中,它随机地“丢弃”一层中的一部分神经元)。这意味着这些神经元的输出被强制设为0,并且在这次前向和反向传播中不参与任何计算。
工作方式:
- 训练时:对于每一个输入样本,网络都相当于在一个不同的、更薄的“子网络”上进行训练。因为神经元是随机被丢弃的,所以每个子网络都需要学会在缺少某些连接的情况下做出正确的预测。这迫使网络学习到更加鲁棒和独立的特征,而不能过分依赖于少数几个神经元。
- 测试/预测时:不再进行Dropout。所有神经元都参与工作,但它们的输出值要乘以训练时的保留概率(例如,如果训练时以50%的概率丢弃,那么测试时该层神经元的输出要乘以0.5),以补偿训练时只有一部分神经元被激活的情况,确保输出的期望值相同。
主要作用:
- 防止过拟合:通过阻止神经元对特定其他神经元的复杂共适应,从而增强模型的泛化能力。
- 提供一种高效地近似组合许多不同神经网络结构的方法:训练一个带有Dropout的网络,可以看作是同时在训练指数级个共享参数的子网络的集合。
蒙特卡洛失活(MC Dropout)
之前的Dropout机制,仅知道其有效果,但是并不清楚具体的原理。Gal 和 Ghahramani 的研究从数学角度证明了Dropout其实是对一个贝叶斯模型进行近似推断。此外他们还提出了MC Dropout,可以提升已有Dropout模型的能力,此外还可以更好地衡量模型的不确定性。
在传统的深度学习中,我们训练一个网络,找到一组最佳的权重参数w,然后用它做预测。贝叶斯方法则认为我们不应该只相信一组参数,而应该考虑所有可能的参数配置w,但根据它们解释数据的能力赋予不同的置信度(即概率)。可是参数空间太大了,无法计算出精确的后验分布。
Gal 和 Ghahramani 的研究证明了,当你用 Dropout 训练网络时,你已经在执行一个复杂的贝叶斯推断任务!你不再是在寻找“唯一最佳”的权重,而是在寻找一个最能描述“哪些权重是合理的”的分布。
而MC Dropout在预测阶段仍然开启Dropout,并进行 T 次前向传播,每次都会得到一个不同的、随机丢弃后的子网络 。通过随机采样和求平均,近似了那个理论上最优的贝叶斯模型平均。
- 求多次预测输出的均值,更加准确和稳定。
- 而多次预测输出的方差,则直接衡量了模型对于这个输入认知的不确定性
因此输出的方差越大,代表着模型的不确定性越强,意味着“我知道我不知道”。在某些医疗、教育等严肃领域,遇到此类情况就应该谨慎对待。
最大范数正则化(Max-Norm Regularization)
对于神经网络中的每一个神经元,将其传入的权重向量的 L2 范数 限制在一个固定的最大值 c 以内。在训练过程中,如果权重向量的范数超过了这个阈值 c,就会被重新缩放,使其范数恰好等于 c。
总结
默认深度神经网络的参数配置建议
| 超参数配置 | 默认设置 |
|---|---|
| 权重初始化 | He初始化 |
| 激活函数 | 较浅:ReLU 较深:Swish |
| 归一化 | 较浅:无需归一化 较深:批量归一化 |
| 正则化 | 早停法 或者 权重衰减 |
| 优化器 | Nesterov加速梯度 或者 AdamW |
| 学习率调度 | 性能自适应调度 或者 单周期调度 |