人工神经网络(Artificial Neuron Network)
人工神经元(Artificial Neuron)
神经元的逻辑计算
一个简单的神经元,需要包含:至少一个二进制输入,一个二进制输出。当一定数量的输入激活后,就会激活输出。比如下图的例子中,需要至少两个输入激活。
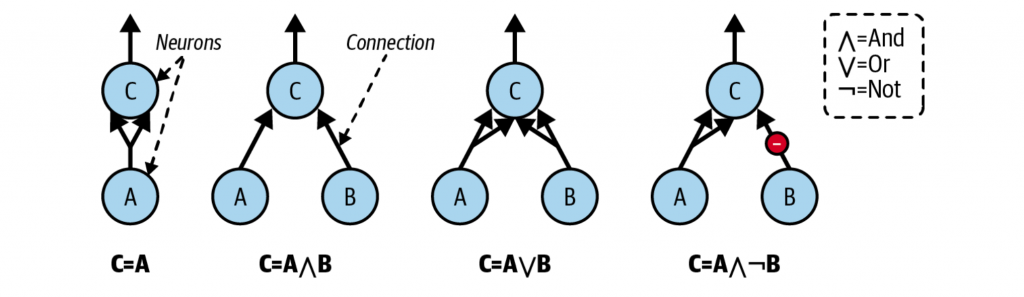
- 第一张图表达的是恒等函数,由于A本身就有两个输入,因此激活A就直接激活了C,等价于C=A
- 第二张图表达的是逻辑与,只有A与B同时激活的时候,才能激活C
- 第三张图表达的是逻辑或,A或者B只要有一处激活,就可以激活C
- 第四张图比较特殊,B的边为抑制作用,因此B激活等价于减少了一个输入。因此这里A激活且B关闭才能激活C
因此通过简单的神经元,可以组装为复杂的逻辑运算。比如逻辑的异或A XOR B,可以通过下图表达出来
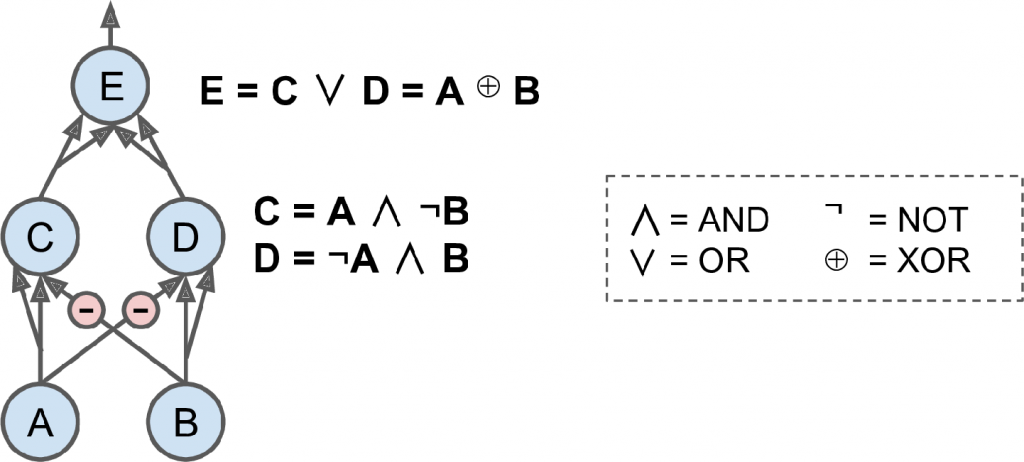
感知机(Perceptron)
感知机是基于完全不同的神经元,阈值逻辑单元(threshold logic unit,TLU)或者叫线性阈值单元(linear threshold unit,LTU)。输入和输出都是数字,而不是之前的二进制形式。
每个输入都会有对应的权重,TLU会先计算线性函数的输出,再根据一个阶越函数(step function)来计算最终的结果。
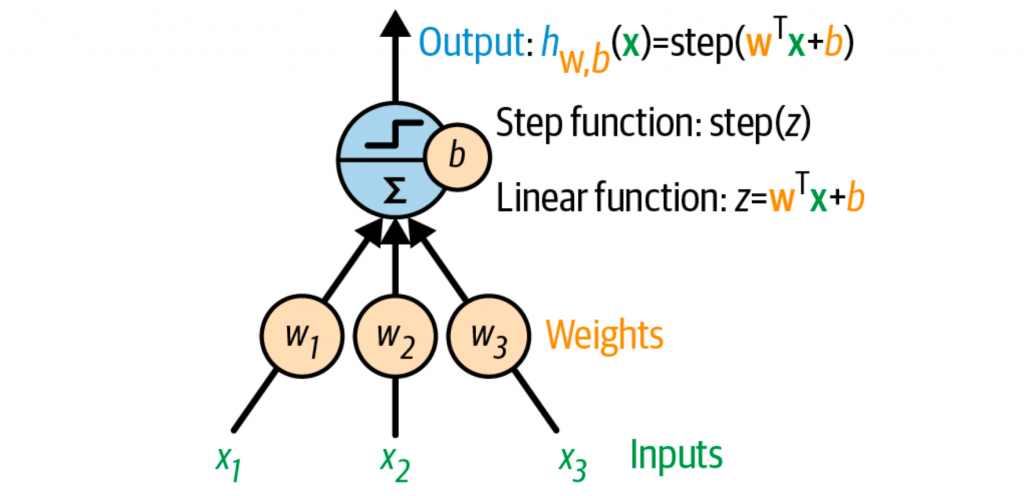
最常用的阶越函数就是单位阶越函数(Heaviside step function),或者用符号函数(sign function)
\text{heaviside}(z)=\begin{cases}
0 &\text{if } z \lt 0 \\
1 &\text{if } z \ge 0 \\
\end{cases}
\qquad
\text{sign}(z)=\begin{cases}
-1 &\text{if } z \lt 0 \\
0 &\text{if } z = 0 \\
+1 &\text{if } z \gt 0 \\
\end{cases}TLU就是要找到合适的w和b,从而让阶越函数的结果正好可以区分不同的分类。
一个感知机在同一层会包含多个TLU,每个TLU就会连接到所有的输入,这种称之为全连接层(fully connected layer),输入组成了输入层(input layer),而TLU的输出组成了输出层(output layer)。
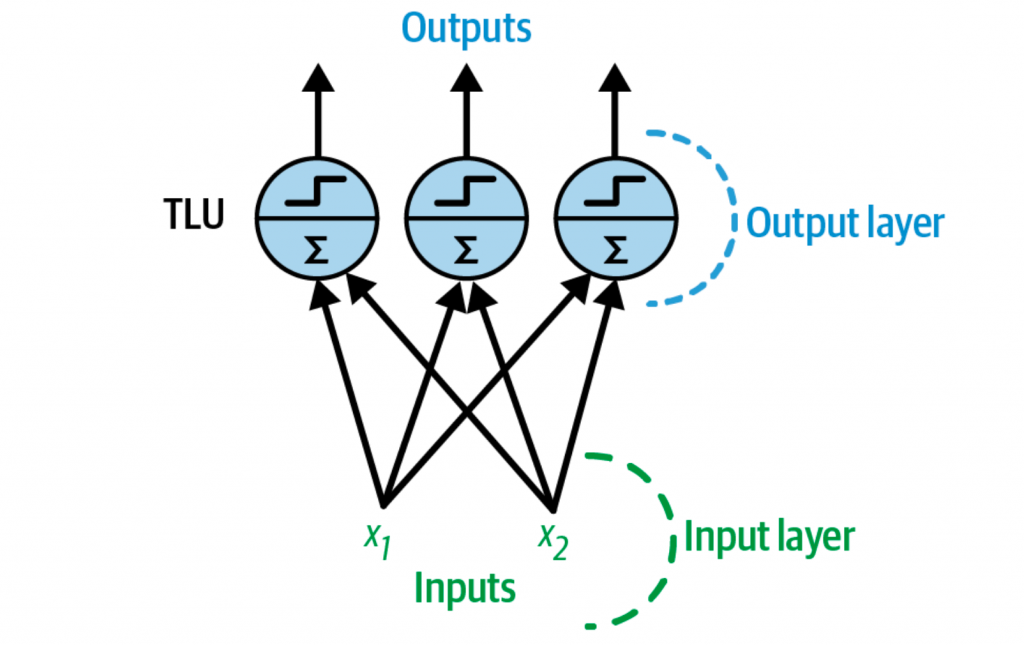
上图中的感知机就会同时训练三个分类器,从而组成了一个多标签的分类器。
全连接层的计算公式如下所示
h_{\bold{W,b}}(\bold{X})=\phi(\bold{XW+b})- X为输入样本矩阵(m × n),m个样本,每个样本n个特征
- W为权重矩阵(n × d),每一行代表一个输入特征,每一列代表一个神经元
- b为偏置矩阵,每一个神经元有一个偏置量
- ϕ为激活函数,当神经元为TLU时,就是一个阶越函数
赫布法则(Hebb’s rule)
该规则由加拿大心理学家 Donald Hebb 提出,其核心思想常被通俗地概括为:
“一起激发的神经元,连接在一起。”
即当两个神经元同步被激活时,它们之间的连接强度会增强。
感知机的训练,其灵感就来源于赫布法则。其训练过程,就是当预测结果错误时,就是增强相关输入的权重,从而让预测结果的误差减少。
w_{i,j}^{(\text{next step})} = w_{i,j}+\eta(y_j-\hat{y_j})x_i- wi,j就是第i个输入特征与第j个神经元之间的连接权重
- xi为当前训练样本的第i个输入特征
- ^yj为第j个神经元的实际输出
- yj为第j个神经元的目标输出
- η为学习率
多层感知机与反向传播
多层感知机(Multilayer Perceptron)
MLP包含1个输入层,1个输出层,而中间会有多层TLU,称为隐藏层(hidden layer)。靠近输入的为lower layer,靠近输出的为upper layer。多层隐藏层堆叠的神经网络,也被称为深度神经网络(deep neuron network,DNN)。
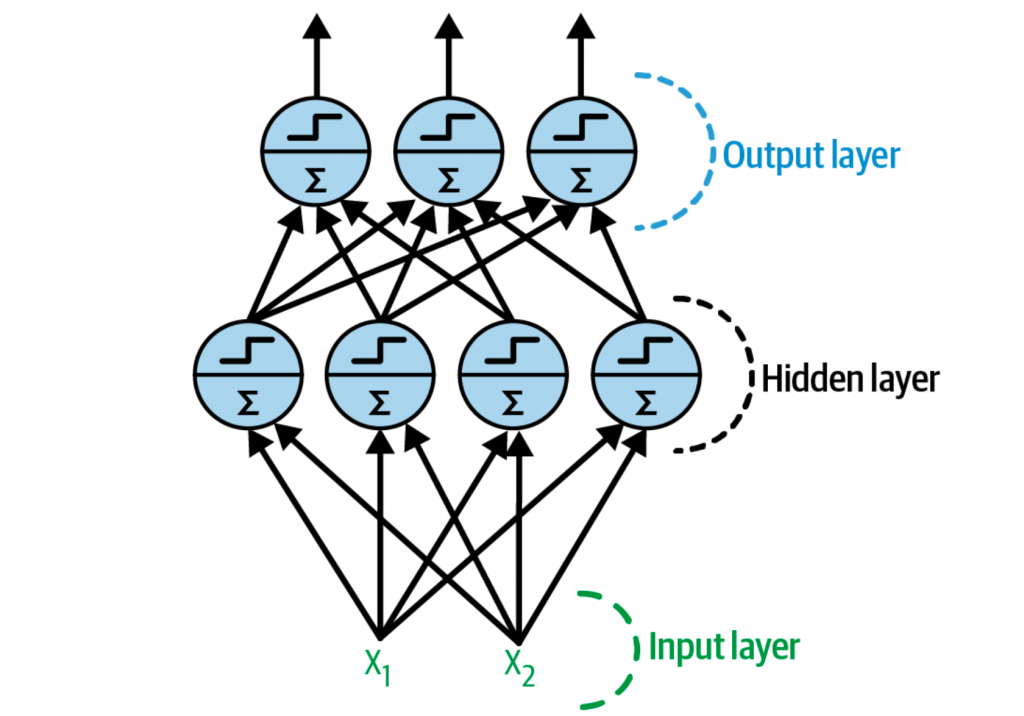
反向传播(backpropagation)
MLP应该如何训练呢?每一层都包含很多参数,再加上多个隐藏层,参数量更是巨大。
反向传播就是用来对MLP进行梯度下降的算法,也就是用链式法则以网络每层的权重为变量计算损失函数的梯度,以更新权重来最小化损失函数。
其详细的过程如下:
- 每次处理一小批数据集(比如32个样本),然后整个样本集会迭代多次,每次称为一个epoch
- 前向传播(forward pass)。将这批样本传入input layer,并计算出结果,再传入下一层,直到最后一层的output layer计算出最终的结果。这个过程和预测过程类似,只不过中间过程的结果也会存下来,节省后续反向传播的计算
- 根据损失函数,计算出整个神经网络的误差
- 然后会计算出误差针对w和b的偏导数(∂L/∂w,∂L/∂b),主要是通过链式法则来进行推导
- 再继续计算下一层,同样利用链式法则,直接计算到输入层
- 最后,通过梯度下降来对权重和偏置量进行微调
不同的激活函数
之前的激活函数是单位阶越函数,其问题取值基本是水平的,其导数大部分情况为0,就没有梯度的存在了。因此我们需要导数不为0的激活函数,才能运用梯度算法,比如说
- sigmoid函数,σ(z) = 1 / (1 + exp(–z)),取值范围是0到1
- 双曲正切函数(The hyperbolic tangent function),tanh(z) = 2σ(2z)-1,取值范围为-1到1。
- ReLU函数(The rectified linear unit function),ReLU(z) = max(0, z)。取值为0处是不可导的,小于0时的导数为0。由于计算速度特别快,因此为默认的激活函数。
三个激活函数及其导数如下图所示
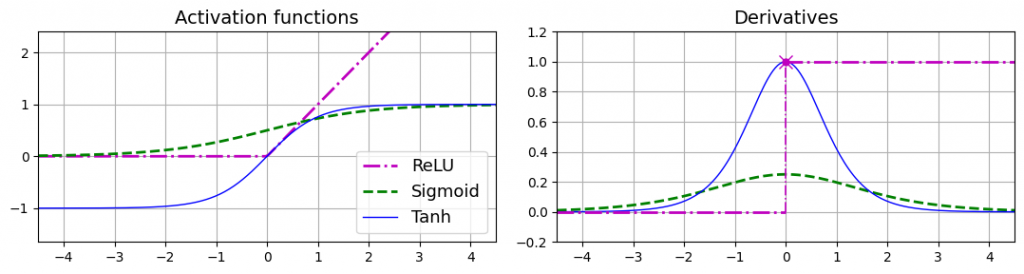
为什么需要激活函数呢?因为多层的线性函数,最终还是一个线性函数。比如f(x) = 2x + 3 与 g(x) = 5x – 1,最终的函数就是f(g(x)) = 2(5x – 1) + 3 = 10x + 1。因此要想表达复杂的非线性关系,就需要激活函数。