AdventOfCode 2023 Day 21 – 天枢星的博客

Part One

从S出发，每一步记录可能到达的点为O，再继续从O出发达到下一个可能的点。最后计算若干步后，所有可能的终点。
...........
.....###.#.
.###.##..#.
..#.#...#..
....#.#....
.##..S####.

比较简单，每一步迭代计算可能的终点即可。

maze

CREATE TABLE maze as 
WITH RECURSIVE maze AS (
  SELECT _row, row_number() over (partition by _row) as _col, pos
  FROM (
    SELECT row_number() over () as _row, unnest(regexp_split_to_array(line, '')) as pos 
    FROM lance_input
  ) t
)
SELECT * FROM maze;

CREATE UNIQUE INDEX idx_maze on maze(_row, _col);

step function

CREATE OR REPLACE FUNCTION step(_count INTEGER)
RETURNS VOID AS $$
DECLARE
    pulse VARCHAR;
BEGIN
    FOR i IN 1.._count LOOP
      UPDATE maze SET pos = t.pos
      FROM (
        SELECT a._row, a._col,
           max(CASE WHEN a._row = b._row AND a._col = b._col THEN '.'
                    WHEN a.pos = '.' THEN 'O'
           END) as pos
        FROM maze a 
        JOIN maze b
        on b.pos IN ('S', 'O')
        AND (
          a._row = b._row AND a._col = b._col + 1
          OR a._row = b._row AND a._col = b._col - 1
          OR a._row = b._row + 1 AND a._col = b._col
          OR a._row = b._row - 1 AND a._col = b._col
          OR a._row = b._row AND a._col = b._col
        )
        GROUP BY a._row, a._col, a.pos
      ) t
      WHERE maze._row = t._row AND maze._col = t._col AND t.pos is not null;
    END LOOP;
END;
$$ LANGUAGE plpgsql;

Part Two

首先是地图横向纵向无限扩展，另一方面步数也是超大数字。
The map repeats infinitely in every direction. The actual number of steps he needs to get today is exactly 26501365.

最小步数方格

先使用第一关中的例子，从原始的迷宫分别横向和纵向扩张成9 * 9的方格，原始迷宫处于这个方格的正中央。计算50步之内每个方格第一次到达的步数。并使用一张stats表来记录每个方格到达的最小步数

CREATE OR REPLACE FUNCTION step(_count INTEGER)
RETURNS VOID AS $$
DECLARE
    pulse VARCHAR;
BEGIN
    FOR i IN 1.._count LOOP
      UPDATE maze SET pos = t.pos
      FROM (
        SELECT a._row, a._col,
           max(CASE WHEN a._row = b._row AND a._col = b._col THEN '.'
                    WHEN a.pos IN ('.') THEN 'O'
           END) as pos
        FROM maze a 
        JOIN maze b
        on b.pos IN ('S', 'O')
        AND (
          a._row = b._row AND a._col = b._col + 1
          OR a._row = b._row AND a._col = b._col - 1
          OR a._row = b._row + 1 AND a._col = b._col
          OR a._row = b._row - 1 AND a._col = b._col
          OR a._row = b._row AND a._col = b._col
        )
        GROUP BY a._row, a._col, a.pos
      ) t
      WHERE maze._row = t._row AND maze._col = t._col and t.pos is not null;

      INSERT INTO stats(step, square, cnt)
      SELECT i, (_row - 1) / 11 * 10 + (_col - 1) / 11, COUNT(*)
      FROM maze
      WHERE pos = 'O'
      GROUP BY (_row - 1) / 11 * 10 + (_col - 1) / 11;
    END LOOP;
END;
$$ LANGUAGE plpgsql;

step(50)之后，就可以得到每个方格到达的最小步数了

postgres=# select step, square, cnt from (select row_number() over (partition by square order by cnt) as rn, step, square,cnt from stats ) t where rn = 1 order by square;
 step | square | cnt 
------+--------+-----
   45 |      3 |   1
   44 |      4 |   2
   45 |      5 |   1
   45 |     12 |   1
   34 |     13 |   1
   33 |     14 |   2
   34 |     15 |   1
   45 |     16 |   1

使用表格来描述，如下所示

			45	44	45
		45	34	33	34	45
	45	34	23	22	23	34	45
45	34	23	12	9	12	23	34	45
44	33	22	7	S	9	22	23	44
45	34	23	12	8	16	27	38	49
	45	34	23	22	27	38	49
		45	34	33	38	49
			45	44	49

从上表中可以分析出

从中心出发，由于障碍物的存在，向四周发散后，步数不会一致。
越往外，规律越发明显。基本都是递增11，因迷宫的四周都是无障碍物的，所以基本上增长11步就达到下一个迷宫。

终点计算

当达到一个方格后，随着步数的增长，终点数会39和42之间来回切换。

postgres=# select * From stats where square = 33;
 step | square | cnt 
------+--------+-----
    1 |     33 |   2
    2 |     33 |   4
    3 |     33 |   6
    4 |     33 |   9
    5 |     33 |  13
    6 |     33 |  16
    7 |     33 |  21
    8 |     33 |  25
    9 |     33 |  29
   10 |     33 |  33
   11 |     33 |  35
   12 |     33 |  40
   13 |     33 |  39
   14 |     33 |  42
   15 |     33 |  39
   16 |     33 |  42
   17 |     33 |  39
   18 |     33 |  42

当步数达到50步后，各个方格的终点数如下所示

 _row |         string_agg         
------+----------------------------
    0 | 00|00|00|06|17|09|00|00|00
    1 | 00|00|06|36|39|38|09|00|00
    2 | 00|06|36|39|42|39|38|09|00
    3 | 06|36|39|42|39|42|39|38|09
    4 | 18|39|42|39|42|39|42|39|15
    5 | 09|38|39|42|39|42|39|29|02
    6 | 00|09|38|39|42|39|29|02|00
    7 | 00|00|09|38|39|29|02|00|00
    8 | 00|00|00|09|15|02|00|00|00
(9 rows)

可以看出，从中心的方格出发，中心方格附近都是39/42交错，越往外，终点数越少。那么计算的时候，先计算39/42这种已经走满方格的，再计算其他的未走满的方格。

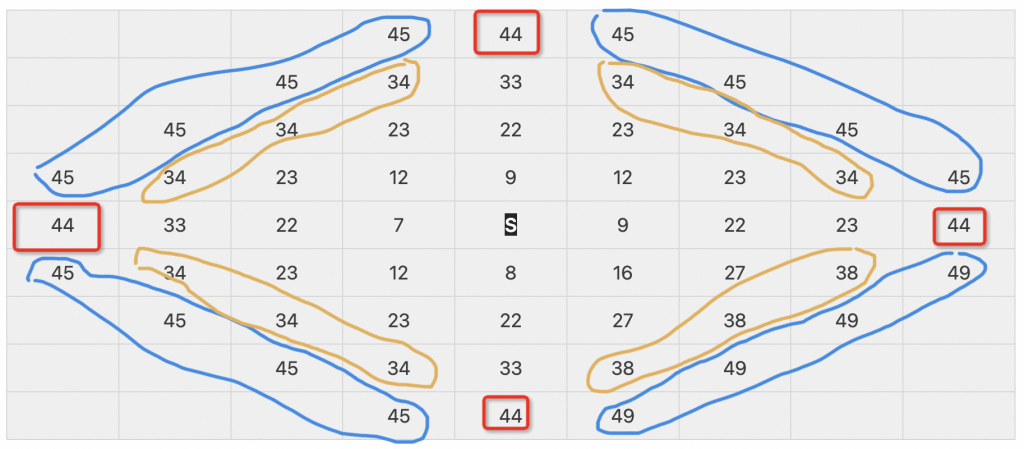
走满的方格中，一共9个42，16个39
未走满的方格中，分为三个部分
- 4个顶点的方格，红色
- 16个斜方向上的方格，蓝色
- 12个斜方向上的方格，黄色

总体相加可以得出：9 * 42 + 16 * 39 + (17 + 18 + 15 + 15) + 4 * (6 + 9 + 9 + 2) + 3 * (36 + 38 + 38 + 29) = 1594

这种方法也是参考了reddit上的一篇文章。

迷宫的快速通道

仔细观察迷宫可以发现，S出发的十字通道畅通无阻，再加上四周也是无障碍物的，因此从中心出发，达到隔壁的迷宫，都是固定的65步，到达左上的隔壁就是131步。

最终结果计算

postgres=# select * From stats where step = 196;               
 step | square | cnt  
------+--------+------
  196 |      0 |  942
  196 |      1 | 5572
  196 |      2 |  939
  196 |  10000 | 5572
  196 |  10001 | 7474
  196 |  10002 | 5577
  196 |  20000 |  958
  196 |  20001 | 5577
  196 |  20002 |  953
(9 rows)

postgres=# select * From stats where step = 327;               
 step | square | cnt  
------+--------+------
  327 |      0 | 6479
  327 |      1 | 7474
  327 |      2 | 6500
  327 |  10000 | 7474
  327 |  10001 | 7407
  327 |  10002 | 7474
  327 |  20000 | 6500
  327 |  20001 | 7474
  327 |  20002 | 6484
(9 rows)

26501365 = 202300 * 131 + 65，向外扩张了202300个方格。
中心方格，偶数步时，终点数为7474；奇数步时，终点数为7407。
红色方格中
- 正上方格，196步时，终点数为5572
- 正下方格，196步时，终点数为5577
- 正左方格，196步时，终点数为5572
- 正右方格，196步时，终点数为5577
蓝色方格中
- 左上方格，196步时，终点数为942
- 右上方格，196步时，终点数为939
- 左下方格，196步时，终点数为958
- 右下方格，196步时，终点数为953
黄色方格中
- 左上方格，327步时，终点数为6479
- 右上方格，327步时，终点数为6500
- 左下方格，327步时，终点数为6500
- 右下方格，327步时，终点数为6484

最终结果为：(202300 – 1)² * 7407 + 202300² * 7474 + (5572 + 5577 + 5572 + 5577) + 202300 * (942 + 939 + 958 + 953) + (202300 – 1) * (6479 + 6500 + 6500 + 6484);