Part One
走迷宫
......F-7..|.|..L-J......
定义迷宫的四种方向 NESW,并从S开始向四个方向前进
SELECT _row, _col, move.next, move.next as full_path
FROM maze, (select unnest(regexp_split_to_array('NSWE', '')) as next) as move
WHERE direction = 'S'
根据当前方向的下一步提示,从而确定后续新的方向
case when m.direction IN ('-', '|') then next_move
when m.direction = 'L' AND next_move = 'W' then 'N'
when m.direction = 'L' AND next_move = 'S' then 'E'
when m.direction = 'J' AND next_move = 'E' then 'N'
when m.direction = 'J' AND next_move = 'S' then 'W'
when m.direction = '7' AND next_move = 'E' then 'S'
when m.direction = '7' AND next_move = 'N' then 'W'
when m.direction = 'F' AND next_move = 'W' then 'S'
when m.direction = 'F' AND next_move = 'N' then 'E'
end as next
根据新方向,确定新的xy坐标
case when next = 'N' then _row - 1 when next = 'S' then _row + 1 else _row end as _row,
case when next = 'E' then _col + 1 when next = 'W' then _col - 1 else _col end as _col
完整SQL
WITH RECURSIVE maze AS (
SELECT _row, row_number() over (partition by _row) as _col, direction
FROM (
SELECT row_number() over () as _row, unnest(regexp_split_to_array(line, '')) as direction
FROM lance_input
) t
),
path as (
SELECT _row, _col, move.next, move.next as full_path
FROM maze, (select unnest(regexp_split_to_array('NSWE', '')) as next) as move
WHERE direction = 'S'
UNION ALL
SELECT _row, _col, next, full_path || next as full_path
FROM (
SELECT p._row, p._col,
case when m.direction IN ('-', '|') then next_move
when m.direction = 'L' AND next_move = 'W' then 'N'
when m.direction = 'L' AND next_move = 'S' then 'E'
when m.direction = 'J' AND next_move = 'E' then 'N'
when m.direction = 'J' AND next_move = 'S' then 'W'
when m.direction = '7' AND next_move = 'E' then 'S'
when m.direction = '7' AND next_move = 'N' then 'W'
when m.direction = 'F' AND next_move = 'W' then 'S'
when m.direction = 'F' AND next_move = 'N' then 'E'
end as next, full_path
FROM (
SELECT case when next = 'N' then _row - 1 when next = 'S' then _row + 1 else _row end as _row,
case when next = 'E' then _col + 1 when next = 'W' then _col - 1 else _col end as _col,
next as next_move, full_path
FROM path
WHERE next is not null
) p
JOIN maze m
ON p._row = m._row
AND p._col = m._col
AND m.direction NOT IN ('.', 'S')
) t
)
SELECT *
FROM path
Part Two
第二部分需要计算出loop内部的方格数,例子中的就是1
......F-7..|.|..L-J......
Point in polygon
这就是典型的Point in polygon问题,将不在pipeline上的用.替代后,打印出来如下图所示。比如红框内的就是满足要求的。

Jordan curve theorem
这里用简单的算法来计算下,就是统计水平线上穿越边界的次数。偶数在边界外,奇数边界内。
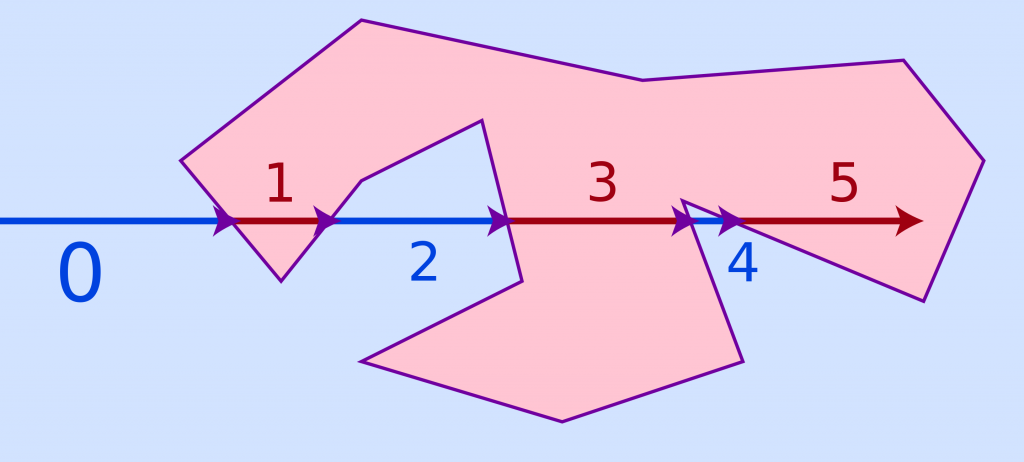
Building borders
原始的输入中,有太多迷惑性的输入,比如FJL7等,可以进行精简下
- F7、LJ,都是U型弯,穿越过去肯定是2次,这里可以忽略。
- FJ、L7,都是竖直方向有2次90弯,但是对于同个水平线上的射线来说,还是一堵墙
- –,水平方向上直接忽略
- S,起点也需要替换为墙
最终SQL
rows AS (
SELECT _row, replace(replace(replace(replace(replace(replace(formatted_row, '-', ''), 'LJ', ''), 'F7', ''), 'L7', '|'), 'FJ', '|'), 'S', '|') as replaced_row
FROM (
SELECT m._row, string_agg(case when p._row is not null then m.direction else '.' end, '' order by m._col) as formatted_row
FROM maze m
LEFT JOIN (select distinct _row, _col from path) p
ON m._row = p._row
AND m._col = p._col
group by m._row
) t
),
x(i) AS (
SELECT 1
UNION ALL
SELECT i + 1 from x
)
SELECT COUNT(*)
FROM (
SELECT substring(x.replaced_row, 1, y.i - 1) as left_str
FROM rows x, (select i from x limit (select max(length(replaced_row)) from rows)) y
WHERE substring(x.replaced_row, y.i, 1) = '.' and y.i > 1
) t
WHERE (length(left_str) - length(replace(left_str, '|', ''))) % 2 = 1;