Part One
根据Sensor和Beacon的坐标,判断某一行有多少个位置不可能有beacon存在
Sensor at x=2, y=18: closest beacon is at x=-2, y=15Sensor at x=9, y=16: closest beacon is at x=10, y=16
Manhattan distance
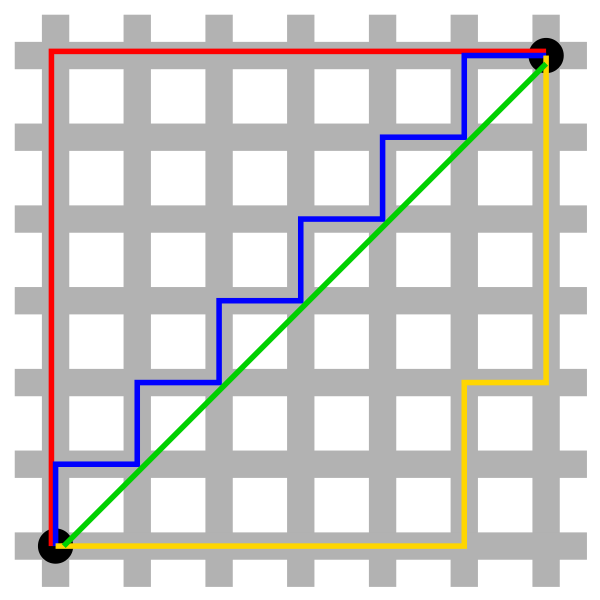
通过计算manhattan distance,再减去垂直距离,就得出了某一行x轴的具体范围
WITH recursive origin AS (
SELECT substring(sensor, 3, strpos(sensor, ',') - 3) :: integer as sensor_x,
substring(sensor, strpos(sensor, 'y=') + 2) :: integer as sensor_y,
substring(beacon, 3, strpos(beacon, ',') - 3) :: integer as beacon_x,
substring(beacon, strpos(beacon, 'y=') + 2) :: integer as beacon_y
FROM (
SELECT id_arr[1][1] as sensor, id_arr[2][1] as beacon
FROM (
SELECT rn, array_agg(id) as id_arr
FROM (
SELECT row_number() over () as rn,
regexp_matches(line, '(x=[-\d]+, y=[-\d]+)', 'g') as id
FROM lance_input
) t
GROUP BY rn
) t
) s
), manhattan AS (
SELECT case when abs(sensor_y - 2000000) > manhattan_distance then null else sensor_x - abs(manhattan_distance - abs(sensor_y - 2000000)) end as min_x,
case when abs(sensor_y - 2000000) > manhattan_distance then null else sensor_x + abs(manhattan_distance - abs(sensor_y - 2000000)) end as max_x
FROM (
SELECT abs(sensor_x - beacon_x) + abs(sensor_y - beacon_y) as manhattan_distance,
sensor_x, sensor_y, beacon_x, beacon_y
FROM origin
) t
)
min_x | max_x
----------+---------
2219242 | 4917380
1532973 | 1597979
-1161321 | 1597979
1156460 | 1296108
3240318 | 3305914
1757114 | 3174874
1597979 | 2084271
1547861 | 1597979
1337377 | 1466069
1368251 | 1597979
(10 rows)
统计beacon位置
最直观的算法,就是通过序列表关联出在范围内x坐标
WITH recursive origin AS (
SELECT substring(sensor, 3, strpos(sensor, ',') - 3) :: integer as sensor_x,
substring(sensor, strpos(sensor, 'y=') + 2) :: integer as sensor_y,
substring(beacon, 3, strpos(beacon, ',') - 3) :: integer as beacon_x,
substring(beacon, strpos(beacon, 'y=') + 2) :: integer as beacon_y
FROM (
SELECT id_arr[1][1] as sensor, id_arr[2][1] as beacon
FROM (
SELECT rn, array_agg(id) as id_arr
FROM (
SELECT row_number() over () as rn,
regexp_matches(line, '(x=[-\d]+, y=[-\d]+)', 'g') as id
FROM lance_input
) t
GROUP BY rn
) t
) s
), manhattan AS (
SELECT case when abs(sensor_y - 2000000) > manhattan_distance then null else sensor_x - abs(manhattan_distance - abs(sensor_y - 2000000)) end as min_x,
case when abs(sensor_y - 2000000) > manhattan_distance then null else sensor_x + abs(manhattan_distance - abs(sensor_y - 2000000)) end as max_x
FROM (
SELECT abs(sensor_x - beacon_x) + abs(sensor_y - beacon_y) as manhattan_distance,
sensor_x, sensor_y, beacon_x, beacon_y
FROM origin
) t
), seq AS (
SELECT (select min(min_x) from manhattan) as id
UNION ALL
SELECT id + 1 as id
FROM seq
WHERE id < (select max(max_x) from manhattan)
), sensor_count AS (
SELECT distinct y.id
FROM manhattan x
JOIN seq y
ON y.id between x.min_x and x.max_x
LEFT JOIN origin z
ON z.beacon_y = 2000000 AND y.id = z.beacon_x
WHERE z.beacon_x is null
)
select count(id) from sensor_count;
可以运行还是比较慢的,主要是笛卡尔积产生的记录数太多导致
count
---------
6078701
(1 row)
Time: 37590.892 ms (00:37.591)
参考AOC 2023年的一个解法,通过计算出slice片段来加速查询
WITH recursive origin AS (
SELECT substring(sensor, 3, strpos(sensor, ',') - 3) :: integer as sensor_x,
substring(sensor, strpos(sensor, 'y=') + 2) :: integer as sensor_y,
substring(beacon, 3, strpos(beacon, ',') - 3) :: integer as beacon_x,
substring(beacon, strpos(beacon, 'y=') + 2) :: integer as beacon_y
FROM (
SELECT id_arr[1][1] as sensor, id_arr[2][1] as beacon
FROM (
SELECT rn, array_agg(id) as id_arr
FROM (
SELECT row_number() over () as rn,
regexp_matches(line, '(x=[-\d]+, y=[-\d]+)', 'g') as id
FROM lance_input
) t
GROUP BY rn
) t
) s
), manhattan AS (
SELECT case when abs(sensor_y - 2000000) > manhattan_distance then null else sensor_x - abs(manhattan_distance - abs(sensor_y - 2000000)) end as min_x,
case when abs(sensor_y - 2000000) > manhattan_distance then null else sensor_x + abs(manhattan_distance - abs(sensor_y - 2000000)) end as max_x
FROM (
SELECT abs(sensor_x - beacon_x) + abs(sensor_y - beacon_y) as manhattan_distance,
sensor_x, sensor_y, beacon_x, beacon_y
FROM origin
) t
), slice AS (
SELECT reduce_dim(num) as range
FROM (
SELECT case when next_num is null OR num + 1 = next_num then array[array[num,num]] else array[array[num, num], array[num + 1, next_num - 1]] end as num
FROM (
SELECT num, lead(num) over (order by num) as next_num
FROM (
SELECT DISTINCT unnest(s.arr) as num
FROM (
SELECT array_agg(min_x) || array_agg(max_x) as arr
FROM manhattan
WHERE min_x is not null
) s
ORDER BY 1
) t
) s
) t
), filter_slice AS (
SELECT distinct x.range
FROM slice x, manhattan y
where y.min_x <= x.range[1] and y.max_x >= x.range[2]
)
SELECT sum(range[2] - range[1] + 1 - beacon_cnt)
FROM (
SELECT x.range, count(distinct z.beacon_y) as beacon_cnt
FROM filter_slice x
LEFT JOIN origin z
ON z.beacon_y = 2000000 AND z.beacon_x between x.range[1] and x.range[2]
group by x.range
) t
这种解法就快多了
sum
---------
6078701
(1 row)
Time: 3.964 ms
Part Two
上一关只是找出了某一行中beacon不可能存在的位置,这一关要求找出具体beacon的位置,要求是所有的sensor都无法观察到
The distress beacon is not detected by any sensor, but the distress beacon must have x and y coordinates each no lower than 0 and no larger than 4000000.
未检测到的beacon
每一个sensor,其覆盖范围是一个菱形。经过第一步的处理,切分为多个slice后,会变成一个个梯形。而这个beacon肯定就藏匿在这几个梯形交叉的空隙处,如下图所示:
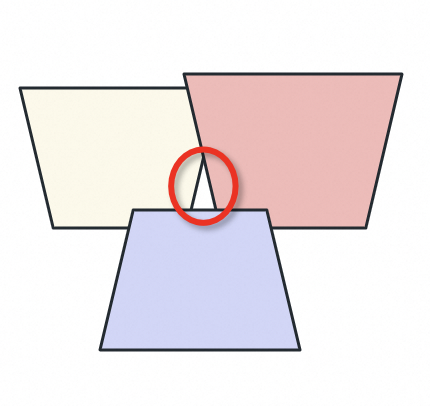
逐行扫描
没有比较好的便捷办法,上一段是检测固定200W行的覆盖记录,将行号作为函数入参,从而检测出每一行的覆盖范围,最后找到唯一一行没有完全覆盖的即可。
CREATE OR REPLACE FUNCTION beacon_calc(line_num INTEGER)
RETURNS INTEGER AS $$
DECLARE
TOTAL_CNT INTEGER;
BEGIN
WITH recursive origin AS (
SELECT substring(sensor, 3, strpos(sensor, ',') - 3) :: integer as sensor_x,
substring(sensor, strpos(sensor, 'y=') + 2) :: integer as sensor_y,
substring(beacon, 3, strpos(beacon, ',') - 3) :: integer as beacon_x,
substring(beacon, strpos(beacon, 'y=') + 2) :: integer as beacon_y
FROM (
SELECT id_arr[1][1] as sensor, id_arr[2][1] as beacon
FROM (
SELECT rn, array_agg(id) as id_arr
FROM (
SELECT row_number() over () as rn,
regexp_matches(line, '(x=[-\d]+, y=[-\d]+)', 'g') as id
FROM lance_input
) t
GROUP BY rn
) t
) s
), manhattan AS (
SELECT case when abs(sensor_y - line_num) > manhattan_distance then null else greatest(0, sensor_x - abs(manhattan_distance - abs(sensor_y - line_num))) end as min_x,
case when abs(sensor_y - line_num) > manhattan_distance then null else least(4000000,sensor_x + abs(manhattan_distance - abs(sensor_y - line_num))) end as max_x
FROM (
SELECT abs(sensor_x - beacon_x) + abs(sensor_y - beacon_y) as manhattan_distance,
sensor_x, sensor_y, beacon_x, beacon_y
FROM origin
) t
), slice AS (
SELECT reduce_dim(num) as range
FROM (
SELECT case when next_num is null OR num + 1 = next_num then array[array[num,num]] else array[array[num, num], array[num + 1, next_num - 1]] end as num
FROM (
SELECT num, lead(num) over (order by num) as next_num
FROM (
SELECT DISTINCT unnest(s.arr) as num
FROM (
SELECT array_agg(min_x) || array_agg(max_x) as arr
FROM manhattan
WHERE min_x is not null
) s
ORDER BY 1
) t
) s
) t
), filter_slice AS (
SELECT distinct x.range
FROM slice x, manhattan y
where y.min_x <= x.range[1] and y.max_x >= x.range[2]
)
SELECT sum(range[2] - range[1] + 1) INTO TOTAL_CNT
FROM filter_slice;
RETURN TOTAL_CNT;
END;
$$ LANGUAGE plpgsql;
查找每一行的覆盖范围,找出未全部覆盖的那一行。总共运行了半小时左右,效率还是比较差的。
postgres=# SELECT id, beacon_calc(id::integer) from generate_series(0, 4000000) as t(id) order by 2 limit 10;
id | beacon_calc
---------+-------------
3400528 | 4000000
2 | 4000001
7 | 4000001
4 | 4000001
5 | 4000001
6 | 4000001
3 | 4000001
8 | 4000001
9 | 4000001
1 | 4000001
(10 rows)
这一行的具体覆盖范围列出来,果然有一列是没有覆盖到的
range
-------------------
{0,0}
{1,2332097}
{2332098,2332098}
{2332099,2696635}
{2696636,2696636}
{2696637,2711961}
{2711962,2711962}
{2711963,3141835}
{3141836,3141836}
{3141838,3141838}
{3141839,3575333}
{3575334,3575334}
{3575335,3618479}
{3618480,3618480}
{3618481,3830893}
{3830894,3830894}
{3830895,3833025}
{3833026,3833026}
{3833027,3999999}
{4000000,4000000}
(20 rows)