下图的例子,来源于sudoku.com。转换为PG中的记录,0代表数字未确定。
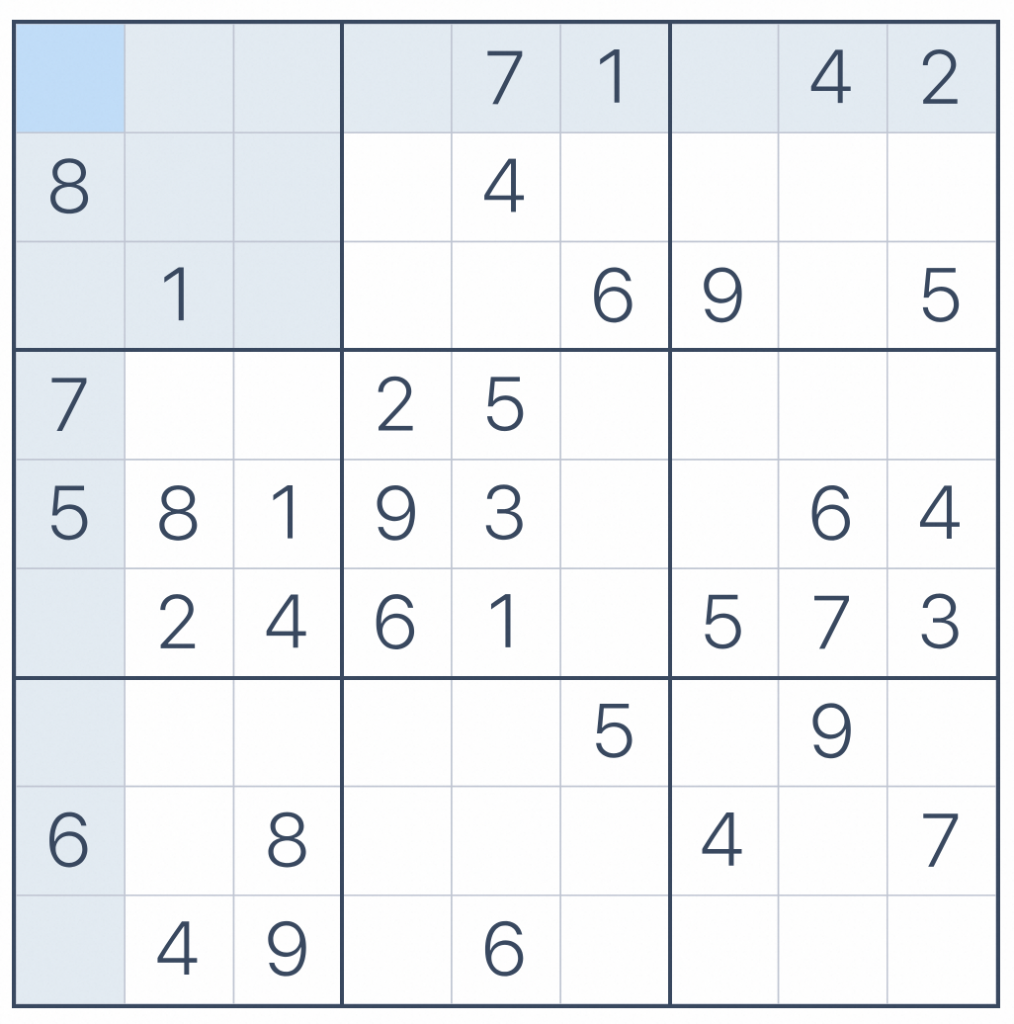
postgres=> create table sudoku(c char(9));
CREATE TABLE
postgres=> insert into sudoku values('000071042'),('800040000'),('010006905'),('700250000'),('581930064'),('024610573'),('000005090'),('608000407'),('049060000');
INSERT 0 9
postgres=> select * From (select substr(c,1,3) as c1, substr(c,4,3) as c2, substr(c,7,3) as c3 from sudoku limit 3 offset 0) t union all select '---','---','---' union all select * From (select substr(c,1,3) as c1, substr(c,4,3) as c2, substr(c,7,3) as c3 from sudoku limit 3 offset 3) t union all select '---','---','---' union all select * From (select substr(c,1,3) as c1, substr(c,4,3) as c2, substr(c,7,3) as c3 from sudoku limit 3 offset 6) t ;
c1 | c2 | c3
-----+-----+-----
000 | 071 | 042
800 | 040 | 000
010 | 006 | 905
--- | --- | ---
700 | 250 | 000
581 | 930 | 064
024 | 610 | 573
--- | --- | ---
000 | 005 | 090
608 | 000 | 407
049 | 060 | 000
(11 rows)
添加grid/row/col属性
原始记录中只有cell中的数字,为了方便后续计算,需要添加grid/row/col属性。grid即9个3*3的方格。
postgres=> -- split to 81 cells with grid/row/col proeperties
postgres=> WITH
postgres-> -- all numbers as integer array
postgres-> all_arr(x) AS (
postgres(> SELECT '{1,2,3,4,5,6,7,8,9}' :: integer[]
postgres(> ),
postgres->
postgres-> -- all numbers as multiple rows
postgres-> all_num(x) AS (
postgres(> SELECT unnest(x) from all_arr
postgres(> ),
postgres->
postgres-> all_cell(_grid, _row, _col, num) AS (
postgres(> SELECT ceil(rn / 3.0) * 10 + ceil(t.x / 3.0) as _grid, rn as _row, t.x as _col, substr(s.c, t.x, 1) :: integer as num
postgres(> FROM (
postgres(> SELECT c,row_number() over () as rn
postgres(> FROM sudoku
postgres(> ) s, all_num t
postgres(> )
postgres-> SELECT * FROM all_cell;
_grid | _row | _col | num
-------+------+------+-----
11 | 1 | 1 | 0
11 | 2 | 1 | 8
11 | 3 | 1 | 0
方格找数字
解数独基本有两大方向,一个方向就是找出这个方格中可能的数字,如果经过排除后只剩下一种可能,那么就确定了方格中的数字。比如方格{5, 6},排除掉row的大部分数字以及grid的2,只剩下7可以填写。
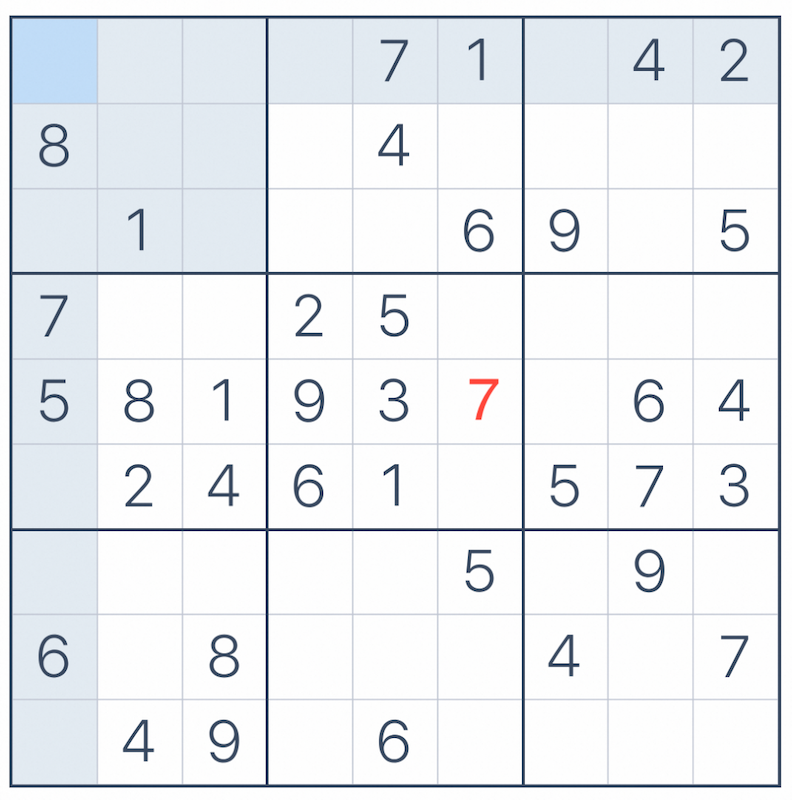
-- find valid numbers in a cell, just filter forbidden numbers of same grid/row/col
cell_to_num(_row, _col, forbid_arr) AS (
SELECT y._row, y._col, uniq(array_agg(x.num)) as forbid_arr
FROM all_cell x
JOIN all_cell y
ON x.num != 0 AND y.num = 0
WHERE x._grid = y._grid
OR x._row = y._row
OR x._col = y._col
GROUP BY y._row, y._col
)
数字找方格
此外,就是找出数字可能的候选方格,如果一个grid中的候选方格只有一种可能,那么也就确定了数字所在的方格。比如数字9,在二排三列的grid中,只能放在{4, 9}方格中。同理,找出同一个row中的唯一候选,以及同一个column的唯一候选。
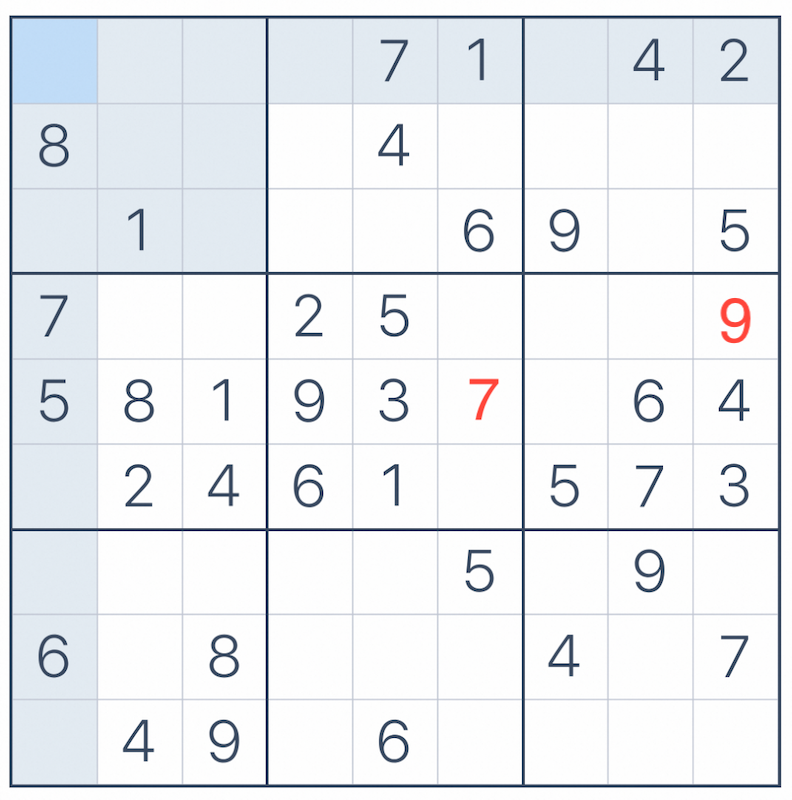
-- find valid cells for a number, only keep records with only one candidate cell for a number
num_cell(num, _grid, _row, _col) AS (
SELECT num, _grid, _row, _col
FROM (
SELECT all_num.x as num, y._grid, y._row, y._col, case when x._grid = y._grid OR x._row = y._row OR x._col = y._col THEN 0 ELSE 1 end as flag
FROM all_num
JOIN all_cell x
ON all_num.x = x.num
JOIN all_cell y
ON y.num = 0
) s
GROUP BY num, _grid, _row, _col
HAVING min(flag) = 1
),
num_to_cell(num, _row, _col) AS (
SELECT num_cell.num, num_cell._row, num_cell._col
FROM num_cell
LEFT JOIN (select _grid, num from num_cell group by _grid, num having count(*) = 1) g
ON num_cell.num = g.num
AND num_cell._grid = g._grid
LEFT JOIN (select _row, num from num_cell group by _row, num having count(*) = 1) r
ON num_cell.num = r.num
AND num_cell._row = r._row
LEFT JOIN (select _col, num from num_cell group by _col, num having count(*) = 1) c
ON num_cell.num = c.num
AND num_cell._col = c._col
WHERE g.num is not null OR r.num is not null OR c.num is not null
)
最终SQL
WITH RECURSIVE sudoku_result(c) AS (
-- original problem
SELECT c :: text
FROM sudoku
UNION ALL
SELECT string_agg(num :: text, '' order by _col) :: text as c
FROM (
-- find num using cell_to_num OR num_to_cell
SELECT _row, _col, case when # valid_arr = 1 then valid_arr[1] when valid_num IS NOT NULL then valid_num else num end as num
FROM (
-- split to 81 cells with grid/row/col proeperties
WITH all_cell(_grid, _row, _col, num) AS (
SELECT ceil(rn / 3.0) * 10 + ceil(t.x / 3.0) as _grid, rn as _row, t.x as _col, substr(s.c, t.x, 1) :: integer as num
FROM (
SELECT c,row_number() over () as rn
FROM sudoku_result
) s, all_num t
),
-- find valid numbers in a cell, just filter forbidden numbers of same grid/row/col
cell_to_num(_row, _col, forbid_arr) AS (
SELECT y._row, y._col, uniq(array_agg(x.num)) as forbid_arr
FROM all_cell x
JOIN all_cell y
ON x.num != 0 AND y.num = 0
WHERE x._grid = y._grid
OR x._row = y._row
OR x._col = y._col
GROUP BY y._row, y._col
),
-- find valid cells for a number, only keep records with only one candidate cell for a number
num_cell(num, _grid, _row, _col) AS (
SELECT num, _grid, _row, _col
FROM (
SELECT all_num.x as num, y._grid, y._row, y._col, case when x._grid = y._grid OR x._row = y._row OR x._col = y._col THEN 0 ELSE 1 end as flag
FROM all_num
JOIN all_cell x
ON all_num.x = x.num
JOIN all_cell y
ON y.num = 0
) s
GROUP BY num, _grid, _row, _col
HAVING min(flag) = 1
),
num_to_cell(num, _row, _col) AS (
SELECT num_cell.num, num_cell._row, num_cell._col
FROM num_cell
LEFT JOIN (select _grid, num from num_cell group by _grid, num having count(*) = 1) g
ON num_cell.num = g.num
AND num_cell._grid = g._grid
LEFT JOIN (select _row, num from num_cell group by _row, num having count(*) = 1) r
ON num_cell.num = r.num
AND num_cell._row = r._row
LEFT JOIN (select _col, num from num_cell group by _col, num having count(*) = 1) c
ON num_cell.num = c.num
AND num_cell._col = c._col
WHERE g.num is not null OR r.num is not null OR c.num is not null
)
-- condition for recursive query terminated. No blank cells.
SELECT x.*, case when x.num = 0 then all_arr.x - y.forbid_arr end as valid_arr, z.num as valid_num
FROM all_cell x
JOIN all_arr
ON 1=1
LEFT JOIN cell_to_num y
ON x._row = y._row
AND x._col = y._col
LEFT JOIN num_to_cell z
ON x._row = z._row
AND x._col = z._col
WHERE exists (select * From all_cell where num = 0)
) s1 order by _row
) s2
GROUP BY _row
),
-- all numbers as integer array
all_arr(x) AS (
SELECT '{1,2,3,4,5,6,7,8,9}' :: integer[]
),
-- all numbers as multiple rows
all_num(x) AS (
SELECT unnest(x) from all_arr
)
SELECT * FROM sudoku_result;
最终的结果如下
c1 | c2 | c3
-----+-----+-----
395 | 871 | 642
862 | 549 | 731
417 | 326 | 985
--- | --- | ---
736 | 254 | 819
581 | 937 | 264
924 | 618 | 573
--- | --- | ---
273 | 485 | 196
658 | 193 | 427
149 | 762 | 358
(11 rows)