无监督学习(Unsupervised Learning)
聚类算法(k-means和DBSCAN)
聚类算法作为无监督学习算法,有广泛的应用场景,比如:
- 客户划分(customer segmentation)。通过网站上的购买、浏览行为等,将客户进行聚类,从而针对每个类别的客户采取不同的市场策略或者推荐。
- 数据分析(data analysis)。对数据集进行聚类后,分析每个类别数据的特征。
- 降维(dimensionality reduction)。通过对一个数据集进行聚类分析后,就可以测量每个样本在每个类别中的亲和度(affinity),也就是与该类别的匹配程度。因此如果聚类结果有k个,最后每个样本就会有k个特征,这样会远远少于之前的特征数。
- 特征工程(feature engineering)。将每个类别的亲和度,作为额外的特征加入到样本集中。
- 异常检测(anomaly detection)。如果一个样本,在所有类别中亲和度都比较低,则说明该样本很可能为异常样本。
- 半监督学习(semi-supervised learning)。如果只有部分样本打标,可以先运行聚类算法,将这些样本的标签扩散到同一个类别中的其他样本,从而让更多的样本拥有标签,提升后续监督学习的表现。
- 搜索引擎(search engine)。比如图片搜索引擎,可以事先通过聚类算法将图片进行分类,图片搜索可以直接返回同一个类别的其他图片。
- 图像分割(image segmentation)。对图片中的像素按照颜色进行聚类,并将每个像素的颜色替换为此类别的中平均颜色,这样可以减少图片中的颜色数,从而方便识别图像中的物体。
k-means
对于下图中的原始样本,可以明显地看出有5个簇。k-means算法,就是计算出每个簇的中心点,并求出每个样本对应最接近的簇。
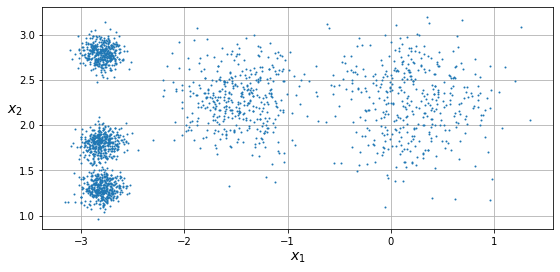
k-means算法
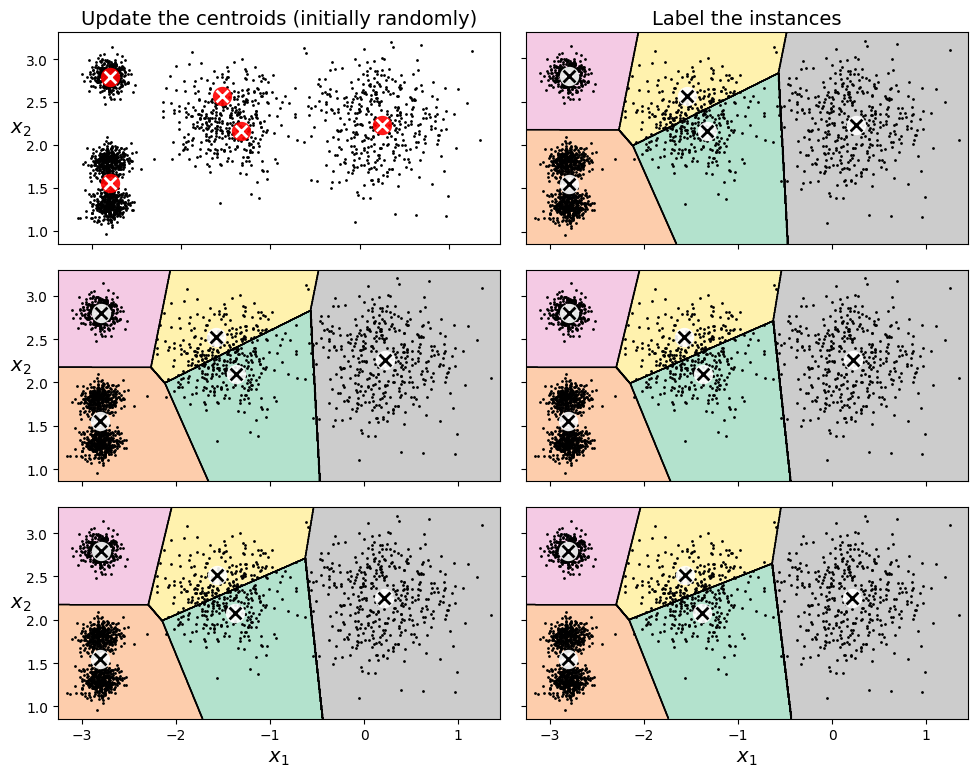
如何确定中心点呢?既然没有太好的手段,只能随机选择若干个样本作为初始中心点。然后计算每个样本最接近的中心点,从而确定每个样本归属的簇。这样就可以更新这个簇的中心点,从而继续这个过程,直到最后中心点不再有变化为止。
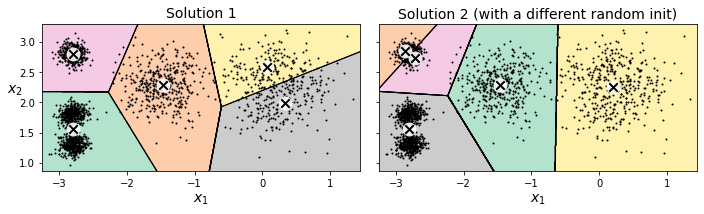
但是k-means算法并不算稳定,初始中心点不同的选择,会导致最终的聚类结果也是大相径庭,仅能得到一个次优解。
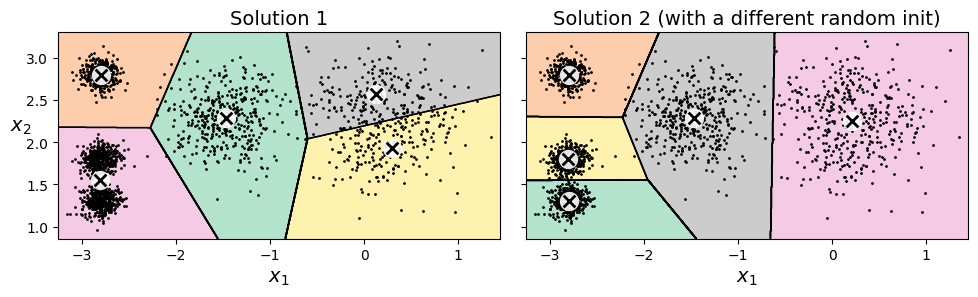
中心点初始化
中心点的选择至关重要,可以事先运行多次初始化,并保留表现最好的那次参数。那么怎么评估表现呢?这里通过一个指标inertia来进行衡量,也就是样本距离其最近中心点的距离之和。inertia越小代表模型表现越佳。
另一种方式就是k-means++算法,其初始化流程如下:
- 随机选取一个点作为中心点
- 从样本中根据概率挑选下一个样本作为中心点,其样本概率的计算方式如下。根据公式可以看出,距离中心点越远,概率越大
- 重复上述步骤,直到选择了k个中心点
p(\bold{x}^{(i)})=\frac{D(\bold{x}^{(i)})^2}{\sum_{j=1}^{m}(\bold{x}^{(j)})^2} \\
\quad\\
D(\bold{x}^{(i)})为\bold{x}^{(i)}距离最近中心点的距离小批量k-means
k-means每次迭代都需要计算全部的样本集,而小批量k-means算法,则可以每次只选取一批样本集来迭代计算中心点,这样可以大大节约计算时间。
根据测试,小批量算法在inertia上的表现会稍逊一筹,但是训练时间大大减少。
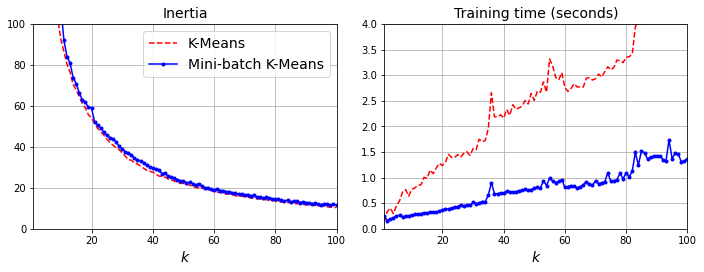
确定最佳的簇数
上文中根据样本分布确定是5个簇,那么如果事先不知道样本分布,那么该如何确定合适的簇数呢?比如之前的样本集,在3个簇和8个簇情况下的表现。
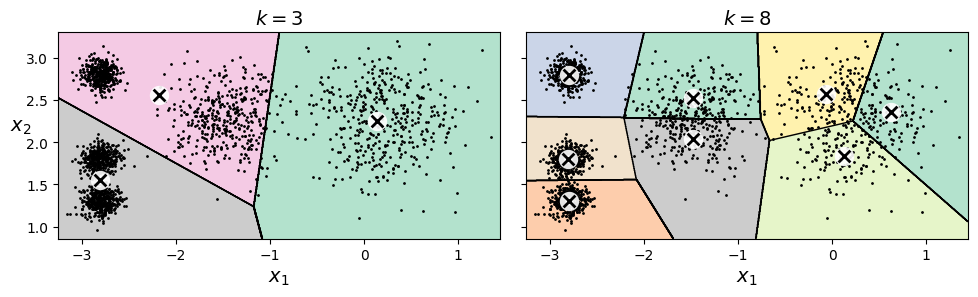
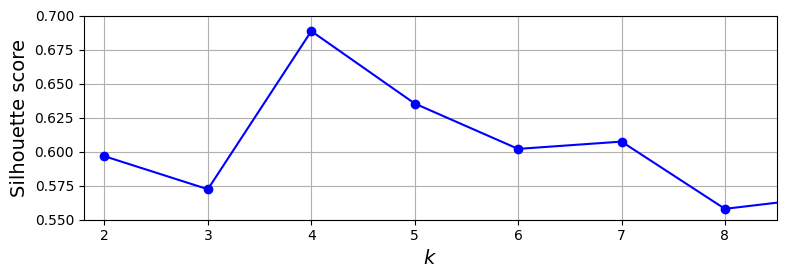
如果从inertia角度来看,簇越多,其值越小,因为其衡量的是样本距离中心的距离。k值与inertia的关系如下图所示,总体走向像一个手肘,从图上看k为4时貌似是个不错的选择。
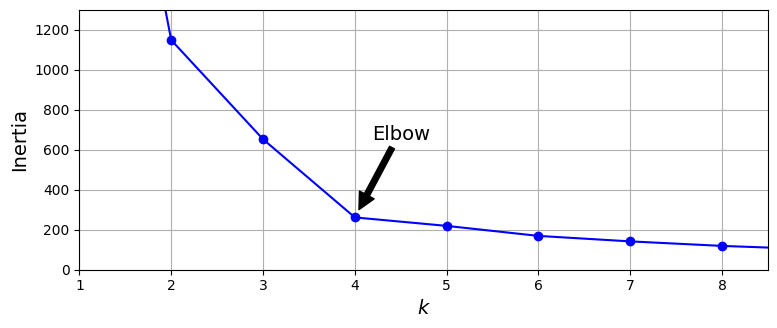
实际上,会使用轮廓系数(sihoutee score)来确定最佳簇的数量。
首先计算某样本i的簇内平均距离a(i)。
a(i)=\frac{1}{|C_i|-1}\sum_{j\in C_i,i \ne j}d(i,j)再计算最近相邻簇的平均距离b(i)。此值越大,说明离其他簇越远。
b(i)=\min_{k \ne i} \frac{1}{|C_k|}\sum_{j\in C_k}d(i,j)最后,样本i的轮廓系数s(i)可以定义为
s(i)=\frac{b(i)-a(i)}{\max(a(i), b(i))} \\
\quad\\
-1 \le s(i) \le 1可以看出,s(i)越接近1,说明该样本越靠近簇中心,远离其他簇。越接近0,说明该样本处于簇之间的边界。如果接近-1,那么说明这个样本很有可能聚类到错误的簇了。
下图就是k取值与轮廓系数的关系图,同样k=4时的效果最好。
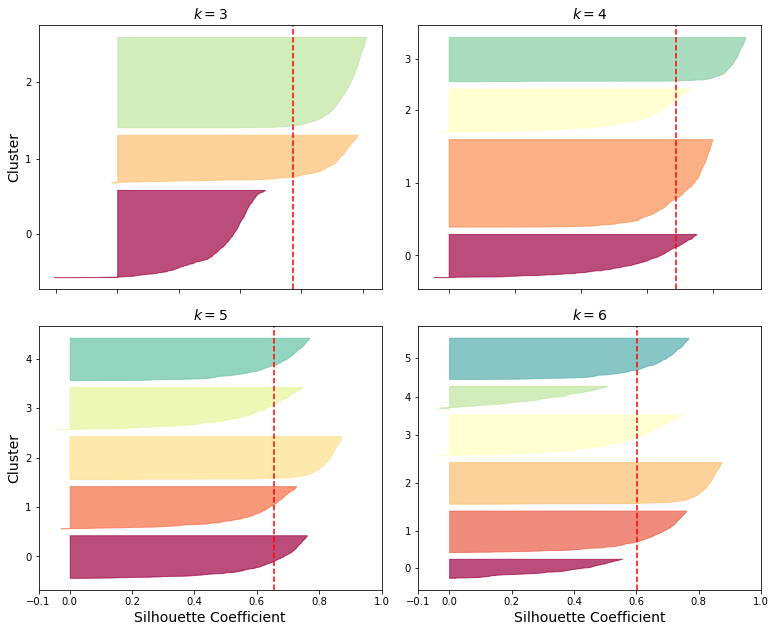
此外,通过轮廓图可能更直观地对比出,k取值对于轮廓系数的影响。图中,同一种颜色代表同一个簇所有样本的轮廓系数从高到低排序,虚线代表轮廓系数的均值。
如果某个簇的轮廓系数整体都在虚线左侧,则说明这个簇的效果不好。最好的聚类结果,就是每个簇的轮廓系数比较接近,这里k=5时的效果最好。
k-means的不足
上文提到,k-means需要运行多次,避免仅找到次优解。此外,还需要找到合适的簇数量。
对于某些样本集,k-means可能还无法正确地聚类,比如下图的聚类结果,两种结果都比较差。
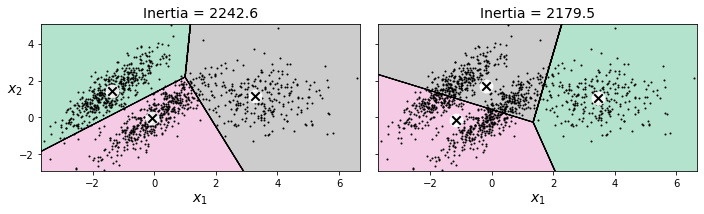
DBSCAN
DBSCAN(density-based spatial clustering of applications with noise)算法是基于样本密度,来找到相邻高密度区域组成的簇。其算法具体如下:
- 对于每个样本,都计算下一小段距离ε内有多少个邻居。
- 如果邻居数(包括自己)超过min_sample,则该样本称为核心点(core instance)。也就是说核心点就是高密度区域的样本。
- 所有核心点的邻居都处于同一个簇内,这些核心点的邻居可能包含其他核心点,从而形成同一个簇。
- 不属于核心点邻居的样本,就被认为是异常点。
如下图所示,红色样本为核心点,B、C虽然非核心点,但是属于核心点的邻居,因此也被包含在同一个簇内。而由于无法从核心点到达N,因此N就视为簇外的局外点。
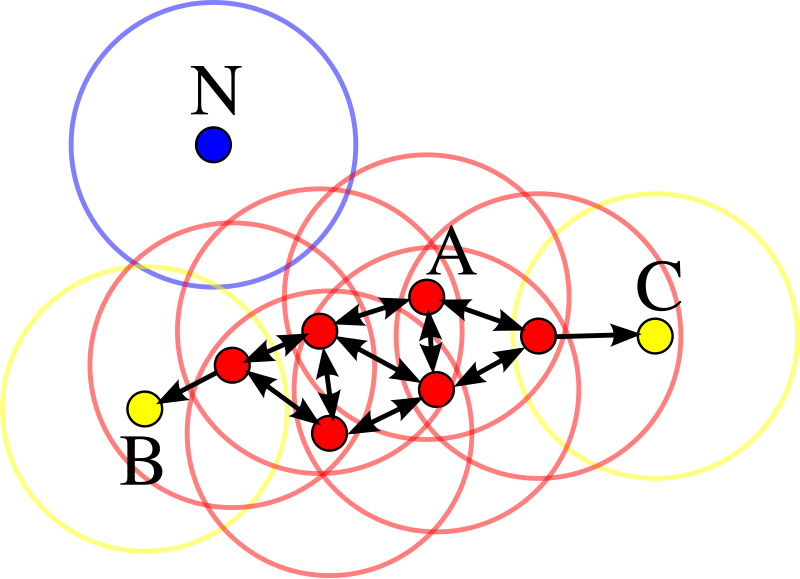
这里的ε参数,会直接影响着聚类的效果。比如下图中,一开始定义的距离很小,导致最终形成了7个簇,且存在不少的异常点。调大到0.20后,聚类结果就比较合理了。
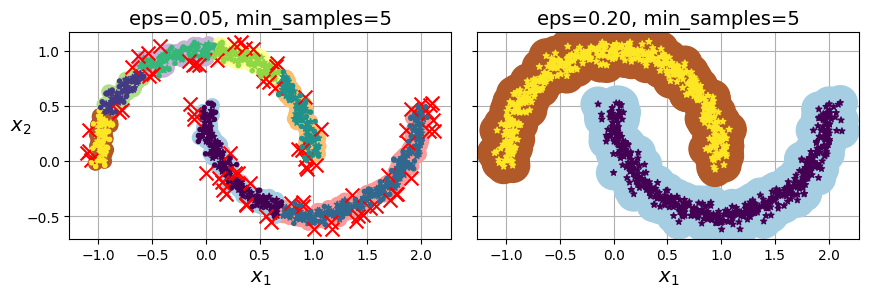
总体而言,DBSCAN算法还是有不少优势的,比如
- 不需要预先申明簇的数量
- 可以找出任何形状的簇
- 可以分辨出异常点
- 仅需要两个参数
其他聚类算法
凝聚层次聚类(Agglomerative clustering)
一种自底向上的聚类算法,从小集群开始,逐渐将其合并,形成更大的集群。
可以想象为一棵二叉树,树的叶子节点就是每个样本。样本之间距离足够近,就合并为小集群,而集群之间距离足够近,又会合并为更大的集群,直到满足条件(数量满足或者距离足够远)。具体如下图所示
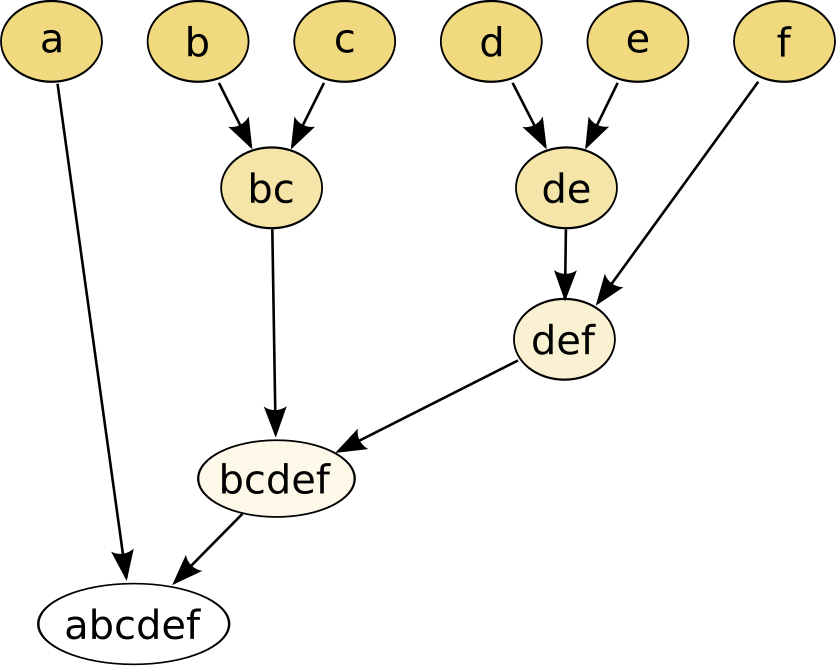
BIRCH
全称是Balanced Iterative Reducing and Clustering using Hierarchies(利用层次结构的平衡迭代规约和聚类)。算法的优势在于能够利用有限的内存资源完成对大数据集的高质量的聚类。
BIRCH 算法的核心思想是:通过一次扫描数据集,就构建一个能够概括数据分布特征的压缩摘要,然后基于这个摘要进行聚类,而不是直接对原始海量数据进行操作。
在BIRCH算法中,每一个数据点用一个CF(Clustering Feature)向量来表示。一个CF向量通常由以下三个部分组成:(子簇的中心点,就是LS / N)
- (N): 该子簇中数据点的数量。
- (LS): 线性和(Linear Sum),该子簇中所有数据点各维度值的线性求和(
N个点的和)。 - (SS): 平方和(Square Sum),该子簇中所有数据点各维度值的平方和(
N个点的平方和)。
这样的好处就是,一方面,两个 CF 可以很容易地合并成一个新的 CF(只需对应相加),这使得合并簇的操作非常高效。另一方面,存储一个 CF 只需要固定大小的内存,远小于存储所有原始数据点。
其工作流程大致分为四步
- 阶段一:构建 CF 树
- 扫描所有数据点,动态地将数据点插入到 CF 树中。
- 对于一个新数据点,从根节点开始,找到距离最近的叶子节点中的子簇。
- 如果将该点加入该子簇后,子簇的半径/直径仍然小于阈值 T,则吸收进去,并更新路径上所有节点的 CF。
- 否则,创建一个新的子簇(CF)。
- 如果节点已满,则进行分裂。这个过程确保了树是平衡的。
- 阶段二:对叶子节点进行凝聚聚类
- 将 CF 树的所有叶子节点(即那些子簇 CF)视为“迷你数据点”。
- 使用一个凝聚层次聚类算法(比如,将距离最近的两个 CF 合并)对这些子簇进行进一步的合并。
- 这一步可以修复因数据输入顺序和树结构限制而可能产生的微小错误分组。
- 阶段三(可选):全局聚类
- 使用阶段二产生的簇中心作为初始点,运行其他聚类算法(如 K-Means)对全部原始数据点进行重新分配。
- 这一步可以进一步提升聚类质量。
- 阶段四(可选):精炼
- 可以再次运行聚类,但这次固定簇的中心,只重新分配数据点,以进行最终优化。
均值漂移(Mean-shift)
Mean-shift算法是一种非参数的聚类算法,它不需要预先指定簇的数量,而是通过数据点的密度分布来自动发现簇的中心。该算法的核心思想是:对于给定的数据点,计算其在一定邻域内(参数h,bandwidth)的均值,然后将该点移动到该均值位置,重复这个过程直到收敛。最终,收敛到同一个点的所有数据点被视为同一个簇。
具体的计算步骤可以分为:
a. Kernel Density Estimation
每个数据点都通过一个核函数来计算其密度概率(后续计算均值的权重),最常用的核函数是高斯核
K(x)=\exp^{-\frac{\|x\|^2}{2}}另外,还可以用最简单的核函数来判断,其实就是邻域内为1,邻域外为0
K(x)=
\begin{cases}
1&\text{if }x \le h \\
0&\text{if }x \gt h
\end{cases}一般还会进行缩放,比如d维空间下的高斯核函数为
K_h(x)=\frac{1}{h^d}K(\frac{x}{h})b. Shifting Data Points
对于任意点,其均值漂移向量为
m_h(x)=\frac{\sum_{i=1}^n K_h(x-x_i)x_i}{\sum_{i=1}^n K_h(x-x_i)} -xc. Convergence and Cluster Identification
最终收敛后(均值漂移非常小),漂移到相同位置的数据点形成了一个簇。
近邻传播(Affinity propagation)
Affinity Propagation(AP)算法是一种基于图论的聚类算法,其核心思想是通过数据点之间的”消息传递”来自动确定簇的数量和中心。
其算法过程包括三个步骤:
a. 构建相似度矩阵
首先构建一个相似度矩阵S,s(i,k)表示数据点k适合作为数据点i的簇中心的相似度。通常使用负欧式距离
s(i,k)=-\|x_i-x_k\|^2 \qquad \text{for }i \ne k而相似度矩阵的对角线,距离为0了。所以一般将对角线s(k,k)称为preference,表示点k称为簇中心的倾向性。如果所有点都设置为median(S),会产生中等数量簇;所有点都设置为min(S),会产生较少簇。也可以每个表设置不同的值
b. 两种消息传播
- 责任度(Responsibility)r(i,k)
从点i发送到候选中心点k,反映点i选择点i作为其中心的累积证据,计算公式如下
r(i,k)=s(i,k)-\max_{k' \ne k}[a(i,k'),s(i,k')]- 可用度(Availability)a(i,k)
从候选中心点k发送到点i,反映点k适合作为点i的中心的累积证据,计算公式如下
\begin{align*}
a(i,k)&=\min[0,r(k,k)+\sum_{i'\notin{i,k}}\max(0,r(i',k))] \\
a(k,k)&=\sum_{i' \ne k}\max(0,r(i',k))
\end{align*}c. 确定簇中心
持续迭代,直到趋于稳定后,对于每个点i,选择使(a(i,k) + r(i,k))最大的k作为其簇中心。
AP算法能够快速收敛的关键在于它建立了一个自增强的正反馈系统,类似于”富者愈富”的马太效应。
a. 消息传递的协同效应
责任度和可用度相互促进,当点k收到很多来自其他点的高责任度时(表示很多点希望k作为中心),这会增加 k的可用度(k变得更加”自信”可以成为中心)。而高可用度又反过来让更多点愿意给k投更高的责任度,这个过程不断自我强化。
b. 竞争排斥原理
同时存在负反馈机制防止所有点都成为中心,在计算责任度的公式中,如果存在一个很强的竞争者k’,那么 k能得到的责任度就会降低,这意味着最终只有少数几个最具竞争力的点能获得足够的支持成为中心。
谱聚类(Spectral clustering)
谱聚类是一种基于图论的现代聚类算法,它通过分析数据点之间的相似性图的谱(即特征值和特征向量)来执行聚类。谱聚类的核心思想就是将聚类问题转化为图划分问题。
之前k-means聚类表现不佳的样本,用谱聚类算法则可以很好分辨,如下图所示
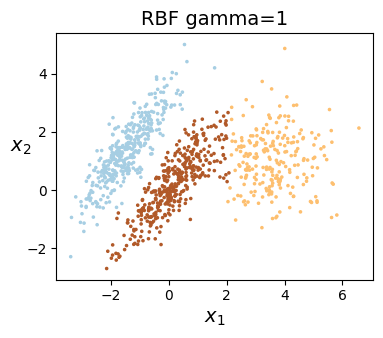
总体步骤分为以下几步:
a. 构建相似度图
相似度矩阵W是一个n×n矩阵,Wij表示xi和xj两个点之间的相似度。最常用的就是用高斯核函数来计算相似度
W_{ij}=\exp(-\frac{\|x_i-x_j\|^2}{2\sigma^2})其中 σ 是尺度参数,控制邻域的宽度。距离越近,相似度越接近1;距离越远,相似度越接近0。
b. 计算拉普拉斯矩阵(Laplacian matrix)
拉普拉斯矩阵定义很简单
L=D-W
W就是上个步骤中的相似度矩阵,D为度矩阵(degree matrix),也是一个对角矩阵。对角线上的值,就是其与其他数据点的相似度之和。
c. 特征分解
计算拉普拉斯矩阵L的前k个最小的特征值及其对应的特征向量。将这k个特征向量(每个是n维向量)按列排列,形成一个n×k 的矩阵U。矩阵U的第i行,可以看作是原始数据点xi在新的k维特征空间中的表示。
d. 在新的特征空间进行聚类
将新特征空间下的数据点,按照k-means等方式进行聚类。
高斯混合模型(Gaussian Mixture model)
高斯混合模型是一个概率模型,它假设所有的数据点都是从若干个高斯分布(参数未知,比如均值、方差等)生成的。根据同一个高斯分布生成的数据点,组成了一个簇(基本都是椭圆形)。
高斯混合模型,就是要根据已知的数据点,找到每个高斯分布,以及其具体的参数。具体计算就是EM算法。
最大期望算法(Expectation-maximization algorithm)
EM算法是一种用于含有隐变量的概率模型参数的迭代优化算法。整个算法分为expectation与maximization这两个步骤。以聚类算法举例,目前已知每个数据点的具体位置,但是缺失的就是每个簇(高斯分布)的具体参数(均值、方差、权重等)信息,因此先确定好簇的个数后,先预设每个高斯分布的初始参数。
a. Expectation步骤
针对每个样本,预测其属于某个高斯分布的概率。
b. Maximization步骤
根据每个高斯分布的所有样本,以及样本归属某个高斯分布的权重,来更新这个高斯分布的参数。然后持续迭代这个过程,直到模型收敛至很小的变化。
EM算法虽然保证收敛性,不过并不保证找到全局最优解,需要多次初始化参数,取结果最好的那次。
高斯混合模型
单个高斯分布,其概率密度函数(PDF)为
P(\bold{x}|\theta)=\frac{1}{(2\pi)^{\frac{d}{2}} |\Sigma|^{\frac{1}{2}} }\exp(-\frac{(\bold{x}-\mu)^T\Sigma^{-1}(\bold{x}-\mu)}{2})- μ为样本均值
- Σ为协方差矩阵
- d为维度
而多个高斯分布的混合模型下,其概率分布就变成了
P(x|\theta)=\sum_{k=1}^K \alpha_k \phi(x|\theta_k)- K为混合模型中高斯分布的数量
- αk为第k个高斯分布的权重因子,权重之和为1,基本就是该高斯分布样本数占总体样本数的比例
- θk为第k个高斯分布的参数,包括均值μk以及方差σk
- ϕ(x|θk)为单个高斯分布的概率密度函数
a. Expectation步骤
依据当前参数,计算单个样本xj属于某个高斯分布k的概率
\gamma_{jk}=\frac{\alpha_k \phi(x_j|\theta_k)}{\sum_{k=1}^K \alpha_k \phi(x_j|\theta_k)} 而对于k来说,所有样本数其概率之和,其实就是归属k的样本数
N_k=\sum_{j=1}^{N}\gamma_{jk}b. Maximization步骤
计算新一轮的参数
\begin{align*}
\mu_k &= \frac{\sum_{j=1}^N \gamma_{jk}x_j}{N_k} \\
\Sigma_k &= \frac{\sum_{j=1}^N \gamma_{jk}(x_j-u_k)(x_j-u_k)^T}{N_k} \\
\alpha_k &= \frac{N_k}{N}
\end{align*}似然函数(Likelihood function)
依然(likelihood)与概率(或然性,probability)在统计学上有明确的区分。概率指的是已知参数后,预测接下来事件发生的可能性;而依然则是根据观测到的结果,推测相关的参数。
比如参数θ确定的情况下,求出现x的概率,其概率函数记为f(x|θ);而已知x出现的情况,来推测参数的可能性,其似然函数记为L(θ∣x)
\mathcal{L}(\theta|x)=f(x;\theta)=P_\theta(X=x)举例来说,有两个高斯分布(均值分别为-4和1)叠加的等高线如下图左上所示,颜色越深代表概率越大。
当确定参数θ=1.3的时候,x的概率密度函数f(x ; θ = 1.3)如下图的左下所示,总面积之和必定为1。
而已知x=2.5的时候,其似然函数L(θ∣x = 2.5)如下图的左上所示,并不遵循概率分布。从红色虚线可以得出,最大可能的参数为1.66左右。
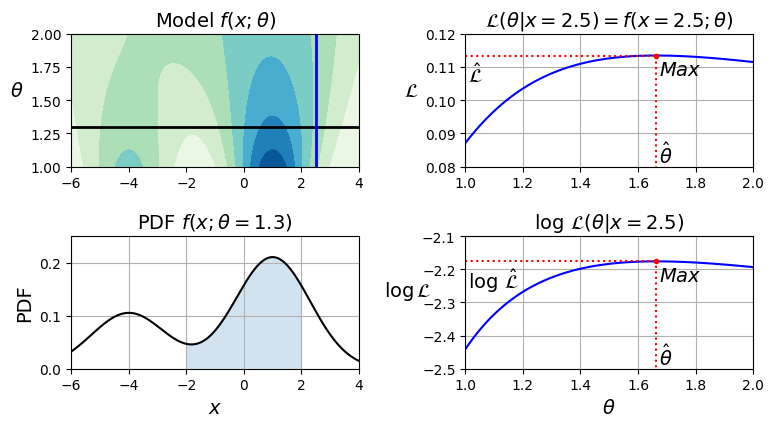
确定簇的个数
之前k-means算法,可以通过轮廓系数来确定最优的簇个数,但是并不使用于高斯混合模型。这里需要使用贝叶斯信息量准则(Bayesian information criterion,BIC)或者赤池信息量准则(Akaike information criterion,AIC),其值越小越好。其定义如下
\begin{align*}
BIC &= \log(m)p-2\log(\widehat{\mathcal{L}}) \\
AIC &= 2p-2\log(\widehat{\mathcal{L}})
\end{align*}- m为样本集个数
- p为模型学习到的参数个数
- L为似然函数的最大值
可见,p越大(模型越复杂,簇越多),其值越大。因此最小化这个值,就可以在模型复杂度与似然函数之间找到平衡。从下图可以得出,簇数为3时的效果最好。