降维(Dimensionality Reduction)
线性代数基础
特征值与特征向量
矩阵乘法可以看作是对向量的一种线性变换,比如
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}
=
\begin{bmatrix}
ax + by \\
cx + dy
\end{bmatrix}对应到几何空间,会有各种的旋转、拉伸等。假如对于一个矩阵A,找到一个向量v,经过线性变换后,其向量仍在同一条直线上(可能反方向,或者改变大小),则v为A的特征向量(eigenvector)。比如下面的例子,向量[1, -1]T经过变换后,变成了[2, -2]T。拉伸了两倍,但是仍然是同一个方向。拉伸的程度,也就是λ,称为特征值(eigenvalue)。
\begin{align*}
\begin{bmatrix}
2 & 0 \\
0 & 2
\end{bmatrix}
\begin{bmatrix}
1 \\
-1
\end{bmatrix}
&=
\begin{bmatrix}
2 \\
-2
\end{bmatrix} \\
\quad\\
A\bold{v}&=\lambda\bold{v} \tag{1}
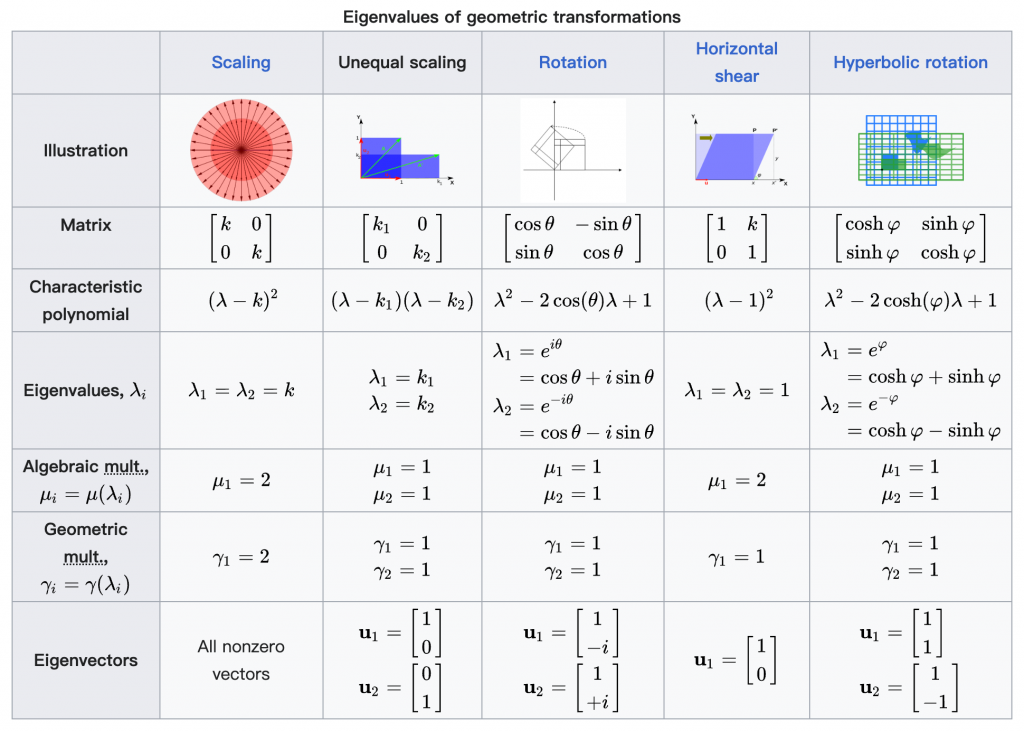
\end{align*}不同矩阵的特征向量
特征分解(EigenValue Decomposition)
对于矩阵A来说,会有不止一个特征向量,假设有m个特征向量组成的特征向量矩阵V,则可以得出
\begin{align*}
A(v_1, v_2, ..., v_m)&=(\lambda_1 v_1, \lambda_2 v_2, ..., \lambda_m v_m) \\
&=(v_1, v_2, ..., v_m)
\begin{bmatrix}
\lambda_1&\dots&0 \\
\vdots&\ddots&\vdots \\
0&\dots&\lambda_m \\
\end{bmatrix} \\
& \text{where } \lambda_1 > \lambda_2 > ... > \lambda_m \\
\quad\\
AV&=V\Lambda \\
A&=V\Lambda V^{-1} \tag{2} \\
\end{align*}上式中,V为特征向量矩阵,Λ为特征值组成的对角矩阵。其中,按照特征值的值排序,特征值越大(说明该特征最明显)放越前面。
最明显的主特征向量,还可以通过以下式子求解得出。经过多次迭代后,最终的结果就是主特征向量线性缩放。
\begin{aligned}
对于任一向量 \bold{x}&=x_1 v_1+x_2 v_2+...+x_m v_m \\
Ax&=A(x_1 v_1+x_2 v_2+...+x_m v_m) \\
&=x_1(Av_1) + x_2(Av_2) + ... + x_m(Av_m) \\
&=x_1(\lambda_1 v_1) + x_2(\lambda_2 v_2) + ... + x_m(\lambda_m v_m) \\
经过k次迭代后\\
A^{k}x&=x_1(\lambda_1^k v_1) + x_2(\lambda_2^k v_2) + ... + x_m(\lambda_m^k v_m) \\
&=\lambda_1^k \left[x_1 v_1 + x_2 \left(\frac{\lambda_2}{\lambda_1}\right)^k + ... + x_m \left(\frac{\lambda_m}{\lambda_1}\right)^k \right] \\
\quad\\
由于\lambda_1 > \lambda_2 > &... > \lambda_m,
\lim\limits_{k\to\infty} \left(\frac{\lambda_i}{\lambda_1}\right)^k=0 \\
因此
\lim\limits_{k\to\infty} A^{k}x&=x_1\lambda_1^k v_1 \\
\end{aligned}特征值及特征向量求解
\begin{aligned}
A\bold{v}&=\lambda\bold{v} \\
A\bold{v}&=\lambda I \bold{v} \\
(A-\lambda I)\bold{v}&=0 \\
左侧矩阵的行列式&必须为0 \\
\det{(A-\lambda I)} &= 0&&(\text{characteristic polynomial})
\end{aligned}举个简单的例子,来说明求解的过程
\begin{aligned}
A&=\begin{bmatrix}
2&1\\
1&2
\end{bmatrix} \\
\det{(A-\lambda I)} &=
\begin{vmatrix}
\begin{bmatrix}
2&1\\
1&2
\end{bmatrix}
-\lambda
\begin{bmatrix}
1&0\\
0&1
\end{bmatrix} \\
\end{vmatrix} \\
&=
\begin{vmatrix}
2-\lambda & 1 \\
1 & 2-\lambda
\end{vmatrix} \\
&=(\lambda-2)(\lambda-2)-1 \\
&=(\lambda-3)(\lambda-1) =0 \\
\implies \lambda_1&=3\\
\lambda_2&=1 \\
\quad\\
(A-3I)\bold{v}_{\lambda=3} &=
\begin{bmatrix}
-1 & 1\\
1 & -1
\end{bmatrix}
\begin{bmatrix}
v_1\\
v_2
\end{bmatrix} =
\begin{bmatrix}
0\\
0
\end{bmatrix} \\
\implies \bold{v}_{\lambda=3} &=
\begin{bmatrix}
1\\
1
\end{bmatrix} \\
\quad\\
(A-I)\bold{v}_{\lambda=1} &=
\begin{bmatrix}
1 & 1\\
1 & 1
\end{bmatrix}
\begin{bmatrix}
v_1\\
v_2
\end{bmatrix} =
\begin{bmatrix}
0\\
0
\end{bmatrix} \\
\implies \bold{v}_{\lambda=1} &=
\begin{bmatrix}
1\\
-1
\end{bmatrix}
\end{aligned}奇异值分解(Singular Value Decomposition, SVD)
上述的特征分解,仅适用于方形矩阵,但是实际中的矩阵大部分非方形矩阵,比如m个样本,n个特征的m*n矩阵。这时就需要用到SVD了,以下内容来源这篇blog。
对于任意向量x,其向量的基为v1和v2,可以表达为基向量的线性组合。
\bold{x}=(\bold{x}\cdot\bold{v}_1)\bold{v}_1 + (\bold{x}\cdot\bold{v}_2)\bold{v}_2 \tag{3}对向量v左乘矩阵M,可以得到
\bold{Mx}=(\bold{x}\cdot\bold{v}_1)\bold{Mv}_1 + (\bold{x}\cdot\bold{v}_2)\bold{Mv}_2 \tag{4}前文提到,矩阵乘法可以看作是对向量的一种线性变换。因此v1和v2经过转换后,在新的向量空间下,其基向量变成了u1和u2
\bold{Mv}_1=\bold{u}_1 \sigma_1 \\
\bold{Mv}_2=\bold{u}_2 \sigma_2 \\代入式(4),即可得出
\begin{align*}
\bold{Mx}&=(\bold{x}\cdot\bold{v}_1)\bold{u}_1\sigma_1 + (\bold{x}\cdot\bold{v}_2) \bold{u}_2\sigma_2 \\
\bold{Mx}&=\bold{u}_1\sigma_1(\bold{v}_1\cdot\bold{x}) + \bold{u}_2\sigma_2 (\bold{v}_2\cdot\bold{x}) \\
\bold{M}&=\bold{u}_1\sigma_1{\bold{v}_1}^T + \bold{u}_2\sigma_2{\bold{v}_2}^T \tag{5}\\
\bold{M}&=\underbrace{
\begin{bmatrix}
\bold{u}_1 & \bold{u}_2
\end{bmatrix}
}_{\text{U}}
\underbrace{
\begin{bmatrix}
\sigma_1 & 0\\
0 &\sigma_2 \\
\end{bmatrix}
}_{\Sigma}
\underbrace{
\begin{bmatrix}
{\bold{v}_1}^T \\
{\bold{v}_2}^T \\
\end{bmatrix}
}_{V^T} \tag{6}
\end{align*}式(6)就是二维空间下SVD分解的简单例子,扩展到多维空间,对于m × n矩阵M,可以分解为
\bold{M}=\bold{U\Sigma{V}}^T \tag{7}- U为m × m 的正交矩阵(orthogonal matrix),其矩阵的列向量称为左奇异向量
- Σ 为m × n 的对角矩阵(diagonal matrix),其对角上的值就是奇异值,从大到小排列
- V为n × n 的正交矩阵,其矩阵的列向量称为右奇异向量
三者具体的作用可以下表来陈述
| 矩阵 | 维度 | 核心作用 |
|---|---|---|
| 右奇异矩阵 V | n×n | 定义新特征空间。它的列是主成分方向,指明了数据中最重要的变化模式。 |
| 左奇异矩阵 U | m×m | 提供样本在新空间中的坐标。它的行是样本点,列是样本在每个主成分上的投影得分。 |
| 奇异值矩阵 Σ | m×n | 标示每个成分的重要性。对角线上的值越大,说明该主成分携带的信息越多。 |
SVD与EVD的关系
上文提到,特征分解仅适用于方形矩阵。对于m × n矩阵X来说,其协方差矩阵XTX,变成了n × n矩阵,就可以使用特征值分解来运算了。
\begin{align*}
\bold{X}&=\bold{U\Sigma{V}}^T \\
{\bold{X}}^T\bold{X} &= (\bold{U\Sigma{V}}^T)^T\bold{U\Sigma{V}}^T \\
{\bold{X}}^T\bold{X} &= \bold{V}{\bold{\Sigma}}^T{\bold{U}}^T\bold{U\Sigma{V}}^T \\
{\bold{X}}^T\bold{X} &= \bold{V}{\bold{\Sigma}}^T\bold{\Sigma{V}}^T \\
{\bold{X}}^T\bold{X} &= \bold{V}{\bold{\Sigma}}^2\bold{{V}}^T \tag{8} \\
\end{align*}将式(8)和式(2)结合起来看,其实SVD就是在寻找协方差矩阵中的特征值(奇异值就是特征值的开方)。特征值越大,协方差越大,数据的差异性越大,此特征向量越重要。
主成分分析(Principal component analysis, PCA)
减少特征空间的维度,但是又不能损失太多信息,因此需要找到样本差异性最大的维度,比如下图中,有三个向量,样本在对应向量上的投影分布是完全不同的。
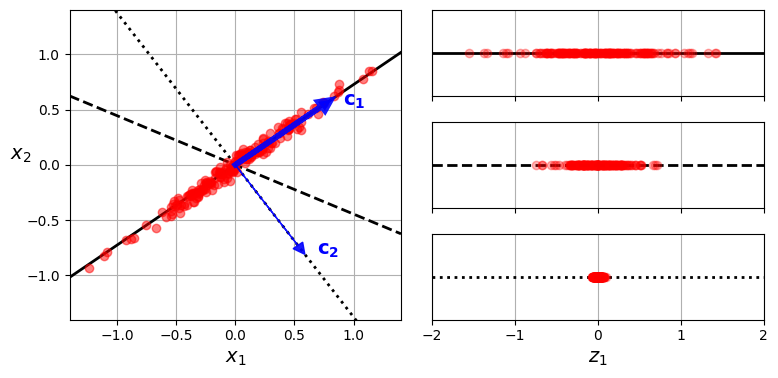
在c1向量上,样本分布最广,差异性保留的最多,因此选择c1作为最重要的特征向量。
那么如果选择其他特征向量呢?应该优先选择与c1正交的其他向量,因为只有正交的向量才能采集到样本剩余的差异性,这里就是c2向量。不正交的话,获取的差异性就会有重叠。
通过SVD进行奇异值分解后,右奇异矩阵V的列向量,就是重要性从高到低的特征向量。降维的过程,就是只选取最重要的k个特征向量,与原始矩阵相乘后,特征数就会从n裁剪到k。
局部线性嵌入(Locally Linear Embedding, LLE)
LLE的背后原理,就是寻找样本与邻居样本的线性关系,然后尝试将样本降维后,看哪种降维方式,能够更好地保留这些线性关系。
举例来说,对于样本集中的某个样本x(i),将其表述为k个邻居的线性函数,如下式所示
f(\bold{x}^{(i)})=\sum_{j=1}^{m}w_{i,j}\bold{x}^{(j)}那目标就是让此函数与实际值的误差越小越好。这里的权重w,只有k个邻居不为0。
\widehat{\bold{W}} = \min_{\bold{W}} \sum_{i=1}^m (\bold{x}^{(i)} - \sum_{j=1}^{m}w_{i,j}\bold{x}^{(j)}) ^ 2 \\
\text{subject to }
\begin{cases}
w_{i,j}=0 & \text{if }\bold{x}^{(j)}不在k个邻居中 \\
\sum_{j=1}^{m}w_{i,j}=0 & \text{for } i = 1,2,..., m
\end{cases}然后将x(i)降维到d维度空间,并且尽可能保留之前的线性关系,即降维后的差异最小。某样本x(i)降维后,变成了z(i),则需要找出这样的z。
\widehat{\bold{Z}} = \min_{\bold{Z}} \sum_{i=1}^m (\bold{z}^{(i)} - \sum_{j=1}^{m}w_{i,j}\bold{z}^{(j)}) ^ 2 \\