集成学习及随机森林
集成学习的大致理念,就是利用“群众的智慧”,通过多个预测模型进行预测,集成多个预测结果,经常可以实现更好的效果。
投票分类器(Voting Classifiers)
这里的做法,就是基于同样的训练集,使用不同的算法,训练出对应的模型。
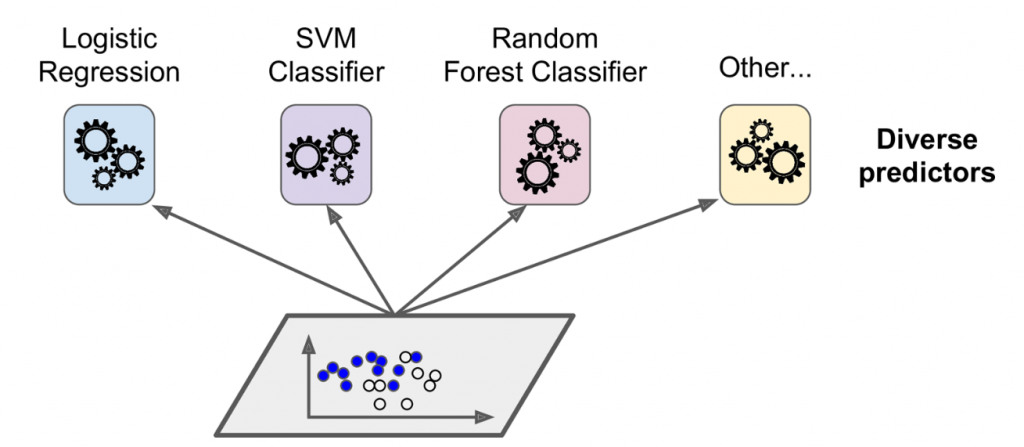
然后基于这些模型的预测结果,投票选出票数最高的结果。
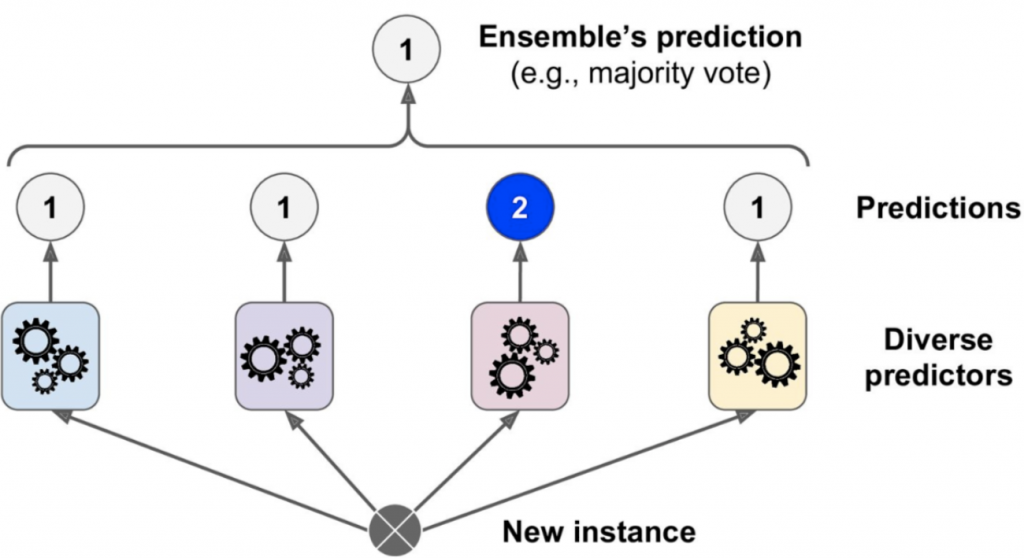
假设一个集成分类器中有1000个分类器,就算每个分类器仅有51%的正确率,基于投票结果也会有超过75%的准确率。但是实际情况下,这些分类器都是基于同样的训练集训练的结果,因此可能会出现同样的识别错误,投票结果大概率也是错误的。
放回取样和不放回取样(Bagging and Pasting)
刚才说的是用不同的算法训练同样的训练集,还可以用同一种算法,来训练样本集的随机取样。放回取样称为bagging,不放回取样称为拿给pasting。
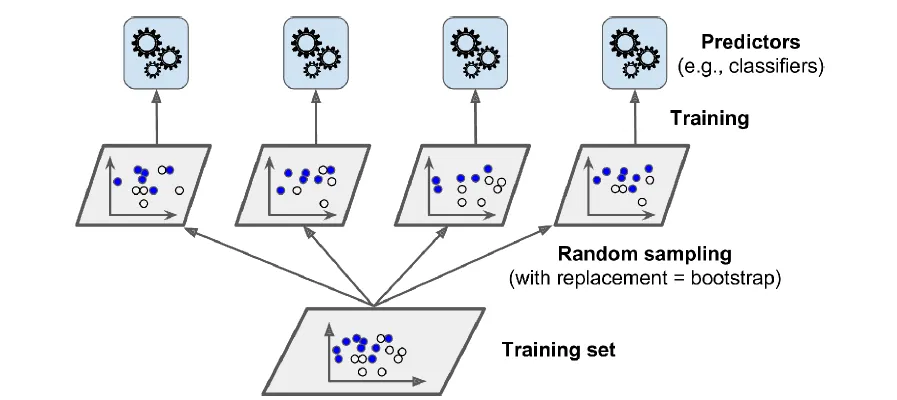
训练好模型后,对于样本进行预测后,再对预测结果进行聚合。从上图可以看出,不同预测模型之间可以并行的训练,也可以并行进行预测,因此有很好的扩展性。
从下图可以看出,集成模型相比于单个模型,偏差(bias)可能会差不多,预测错误率上相差无几。但是variance(方差)上来看,集成模型表现更好,其边缘更为平滑。
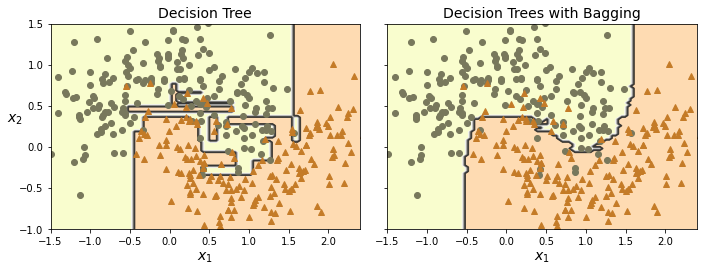
相比于不放回取样,放回取样会增加更多的多样性,因此不会导致过拟合,模型表现会更加好。
随机森林(Random Forest)
随机森林,是决策树模型的一个集成。随机森林算法,在生成决策树的时候,引入了额外的随机性,在挑选特征的时候并没有根据代价函数选择最佳的特征,而是从几个特征中挑选其中的最佳特征。
在生成树的时候,引入随机的特征以及随机的阈值,会生成非常随机的决策树。这种非常随机的树,称为极端随机树(Extremely Randomized Trees,简称Extra-Trees)。相比于之前的决策树算法,更加随机避免过拟合,而且有更快的生成速度。
此外,决策树模型中,越重要的特征越靠近根节点,越不重要的特征越靠近叶子节点。因此,可以计算随机森林中特征的平均深度,来决定该特征的重要程度。
提升(Boosting)
Boosting指的是一种将几个较弱的学习器,集成为一个强大的学习器。基本理念,就是顺次训练模型,并尝试对上个模型进行纠错。目前较为流行的有AdaBoost(Adaptive Boosting)和Gradient Boosting。
自适应提升(Adaptive Boosting)
一个有效纠错的办法,就是针对上个模型的未拟合样本,当前模型需要特别的“重视”,从而持续改善效果。
从上一个分类器的分类结果中,找出那些分类错误的样本,这些样本的权重会得到提升(Boost),从而在下一个分类器训练时进行特殊对待。
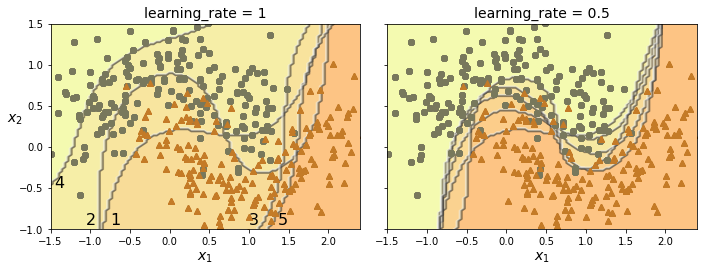
下图就是自适应提升的效果。左图中第一次预测会有部分样本预测错误,在第二次训练的时候,就会特别对待这些错误样本,确保其预测正确。但是,后续的训练可能会矫枉过正,为了确保某些样本预测正确而忽略其他样本,比如后面的三个模型,其预测的正确率就很离谱了。但是集成学习的投票机制,会挑选预测结果中的多数选择,因此单个分类器准确率低,并不会太影响最终准确率。
从左右的图对比也能看出,学习率越低越“保守”,不会有特别离谱的分类结果。
此方法的缺点就是无法并行化,因为必须依赖上一个模型的验证结果。
AdaBoost算法
其算法最重要的就是提升出错样本的权重,这里的权重会影响下次训练的结果。比如优先挑选权重高的样本到训练集中,或者决策树模型会根据样本权重来计算代价。
m个样本的初始权重都是1/m,每个预测模型的错误率基于下式计算
\begin{aligned}
r_j=\sum_{\substack{i=1\\ \widehat{y_{j}}^{(i)} \ne y^{(i)}}}^{m} w^{(i)} \bigg/ \sum_{i=1}^{m}w^{(i)}
&&\quad \widehat{y_{j}}^{(i)} \text{为第i个样本在第j个模型中的预测结果}
\end{aligned} 本预测模型的权重αj可以通过下式计算得出,其中η就是上图中的学习率。可以看出,模型越准确,权重越高。如果错误率接近50%,则结果越接近0。
\alpha_{j}=\eta \log \frac{1-r_j}{r_j}然后,上次分类错误的样本权重,就会根据下式进行更新。可见,如果预测结果错误,权重就会得到提升。
\text{for }i=1, 2, ..., m\\
\quad\\
w^{(i)} \gets
\begin{cases}
w^{(i)} & \text{if } \widehat{y_j}^{(i)} = y^{(i)} \\
w^{(i)} \exp(\alpha_j) & \text{if } \widehat{y_j}^{(i)} \ne y^{(i)}
\end{cases}这些权重提升后的样本,会用于下个模型的训练。整个过程会持续迭代,直到训练出足够数量的模型。
而将模型用于预测时,仅需要集成所有模型的预测结果,并添加上模型的权重,最后挑选出投票结果最高的预测结果。
\widehat{y}(\bold{x})=\max_{k} \sum_{\substack{j=1 \\ \hat{y}_j(x)=k}}^{N}\alpha_j \qquad \text{N为预测模型数}梯度提升(Gradient Boosting)
梯度提升,也是类似自适应提升,依次添加模型,并逐渐修复前个模型的错误。不同的是,该方法并不是去调整权重,而是每个模型会尽量去拟合上个模型的残差(residual errors)。
通过一个决策树模型来说明此方式的大致原理,这个决策树称之为梯度提升回归树(GBRT)。
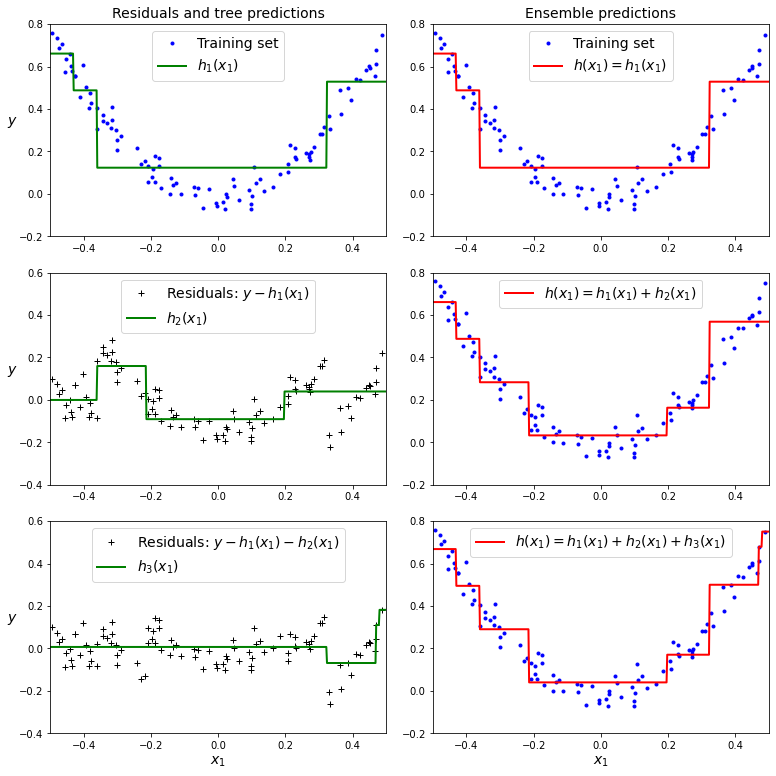
下图中,左侧为单独的预测模型,而右侧为多个模型的集成预测结果。左侧第一张图,就是用决策树模型拟合的结果。左二和左三,就是根据上一个模型的残差去拟合的结果。
而右图则是集成多个模型的预测结果,集成的方式就是将多个模型的预测结果进行相加。可见随着集成的模型越来越多,其拟合也越来越准确。
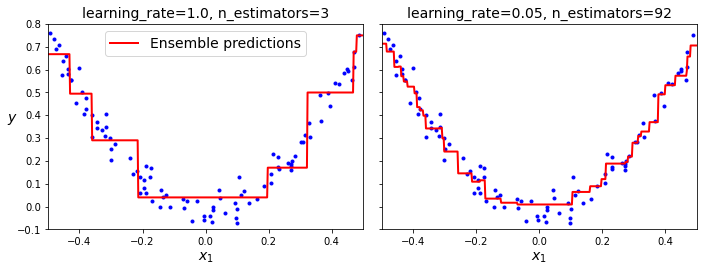
学习率是用来控制每棵树的贡献度,学习率越低,就需要更多的树来构建一个集成的模型。下图可以看出,当学习率低且树的数量足够时,其模型的拟合效果更好。
堆叠法(Stacking)
堆叠法的理念,就是与其使用各种方法(比如投票法)来聚合多个模型的预测结果,还不如直接基于预测结果训练一个模型出来。其实现原理,就是基于训练集训练多个基础模型,并将模型预测结果作为特征,再去训练一个元模型(meta learner)。
常见的做法,就是将训练集分拆为2个子集。其中,子集1用于训练基础模型,如下图所示:
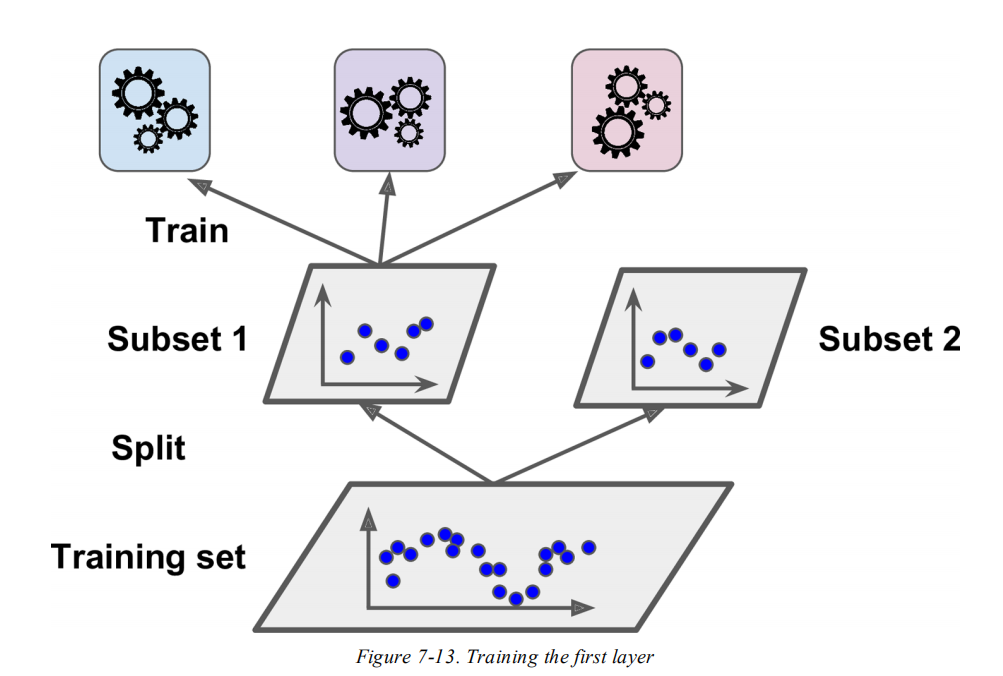
然后用这些模型预测子集2,每个模型的预测结果作为特征(多少个模型就有多少维特征),从而构成一个新的训练集来训练元模型。
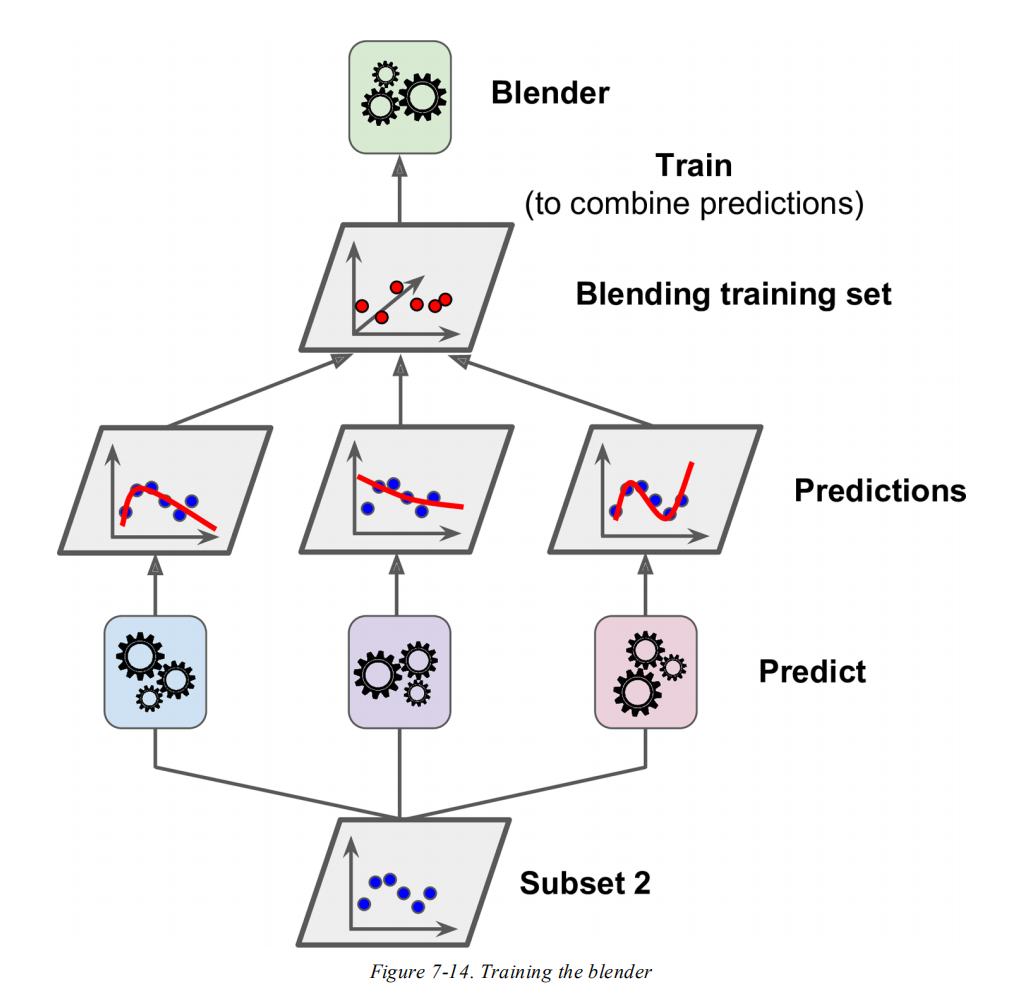
当然,堆叠法也可以堆叠多层,用第一层的预测结果训练第二层,再用第二层的预测结果训练第三层,以此类推。