Decision Tree
决策树分类
决策树模型
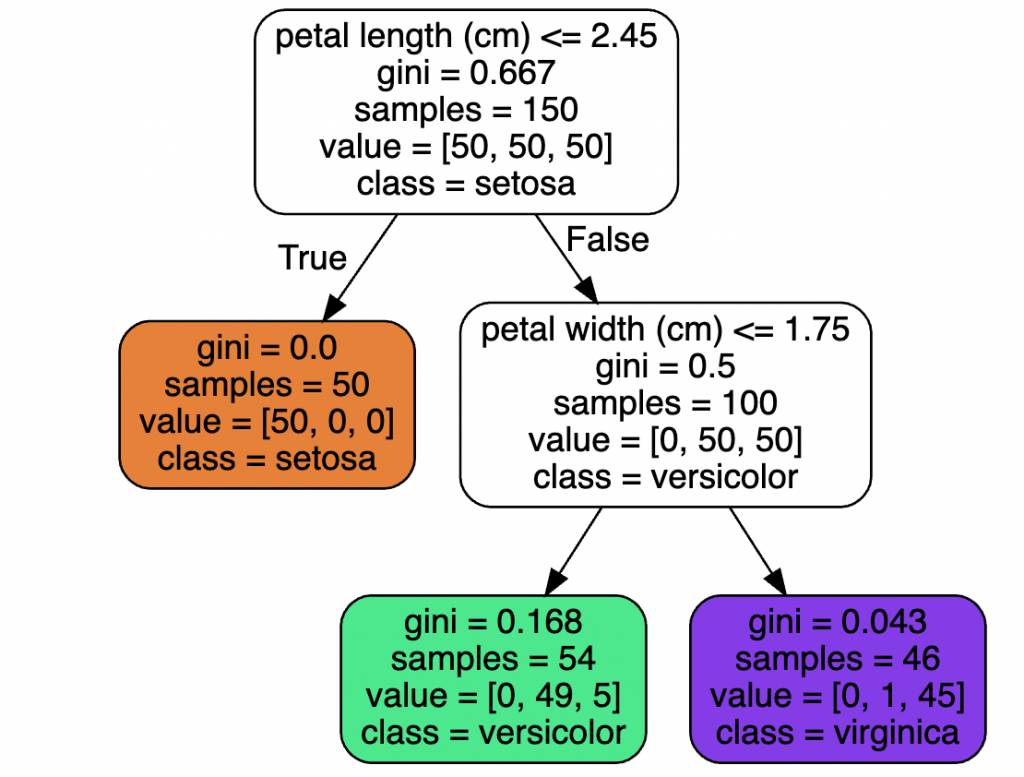
上图就是一个简单决策树模型的可视化展示,每个节点中的属性定义如下:
- samples:有多少样本数符合当前节点的条件
- values:上述的样本数中,在对应每个分类的样本数
- class:此节点对应的分类
- gini:此节点的纯度,gini=0时,所有的样本都是同一个分类
Gini纯度的计算方式如下:
G_i=1-\sum_{k=1}^{n}{p_{i,k}}^{2}\\
\quad\\
p_{i,k}就是分类k在节点i中的占比决策树在二维空间内的可视化如下图所示,其中Depth为决策树中的层级,分界线就是在某个特征上的判断阈值,此分界线将一个区域划分为更小的两个区域。
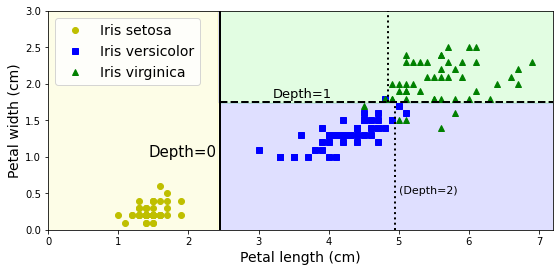
从上图可以看出,决策树模型非常好解释,也被称为白盒模型(white box models)。
CART算法
CART(Classification And Regression Tree)算法可以用来训练决策树,其原理也非常简单,挑选一个特征k,根据阈值tk来训练集拆分为两个子集。但是要如何挑选合适的特征以及阈值呢?最合适的拆分,就是拆分出最纯净的子集。其代价函数如下:
J(k, t_k)=\frac{m_{left}}{m}G_{left} + \frac{m_{right}}{m}G_{right}\\
\quad\\
\text{where}
\begin{cases}
G_{left/right} \quad 左右子集的纯度\\
m_{left/right} \quad 左右子集的样本数
\end{cases}最小化代价,其实就是子集的纯度与样本占比的一个权衡,从而避免纯度虽高但是占比很低的拆分。其训练过程就是一个迭代拆分子集的过程,其持续迭代直到最大深度,或者找不到更纯的子集了。
另外可以看出,CART算法是一个贪婪算法,每次迭代都是寻求当前层级的最优解,其他层级同样仅寻找当前最优,因此最终的模型仅仅是一个不错的解法,并不一定是全局最优解。
计算复杂度
当模型用于预测的时候,需要用根节点遍历到叶子节点。决策树大约是一个平衡树,从根节点到叶子节点,大约的计算复杂度为O(log2(m))。每次判断仅需要对比某一个特征,因此与特征数无关。即使样本数很大,也不会有太长的预测时间。
在训练的时候,训练算法需要对比所有的特征,因此训练复杂度大约为O(n * m log(m))。
信息熵
熵用来定义信息的复杂度,当一个样本中的信息都相同时,熵为0。用于决策树分类时,当一个样本集都是同一个分类时,熵为0。决策树的熵定义如下,可以用来替代纯度。
H_i=-\sum_{k=1}^{n}p_{i,k}\log(p_{i,k})\\
\text{subject to }p_{i,k}\ne0正则化超参数
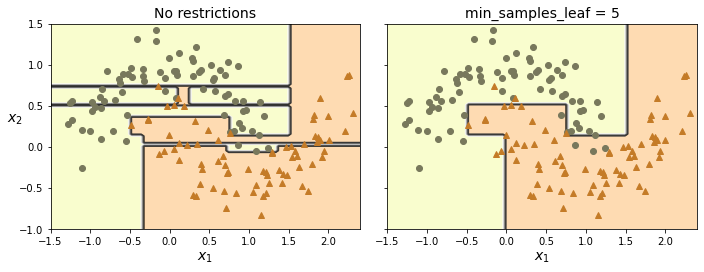
通过超参数来正则化,避免模型的过拟合,比如:
- min_samples_split:拆分之前最小的样本数
- min_samples_leaf:叶子节点的最小样本数
- max_leaf_nodes:最大的叶子节点数
决策树回归
回归模型

回归模型与分类模型很类似,区别就是每个叶子节点并不是预测一个分类,而是预测一个具体的值。 每个叶子节点中的value,就是该节点所有样本的平均值,MSE就是该节点所有样本的均方误差。
拿一个简单的单一特征举例,其决策树回归模型如下所示。图中,每个叶子节点的预测值,就是红色实线。因此分类越精细,y的预测值,也就是红色实线,就越拟合样本。
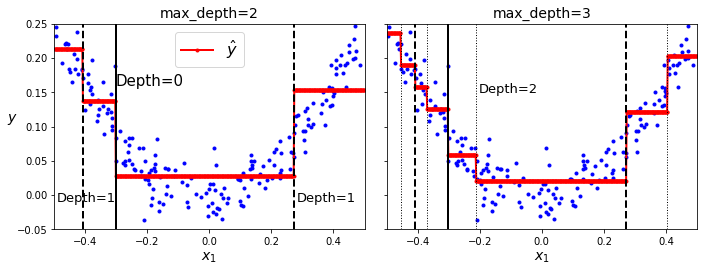
回归算法的目的,就是让每个子集中的样本尽量靠近在一起,这样预测值才不会偏离训练集的值。这时的代价函数就转变为最小化均方误差。
J(k, t_k)=\frac{m_{left}}{m}\text{MSE}_{left} + \frac{m_{right}}{m}\text{MSE}_{right}\\
\quad\\
\text{where}
\begin{cases}
\text{MSE}_{node} =\sum_{i\in node}(\hat{y}_{node}-y^{(i)})^2\\
\hat{y}_{node} =\frac{1}{m_{node}}\sum_{i\in node}y^{(i)}
\end{cases}同样,可以通过参数来控制正则化的度,避免过拟合
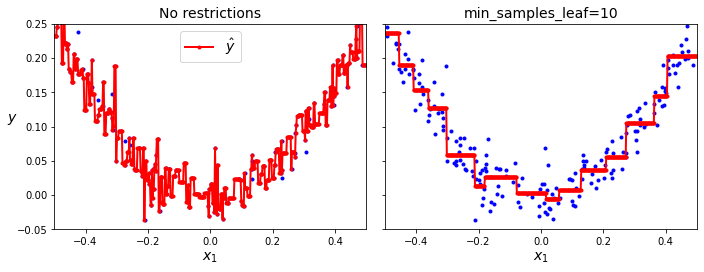
不稳定性
决策树模型简单高效,且可解释,但是存在一些限制或者说不足。
首先就是决策树的分类边界,必须与坐标轴平行(因为是根据某个特征的阈值进行判断),因此当样本集的分离边界不是平行坐标轴,则模型会变得非常复杂,如下图所示
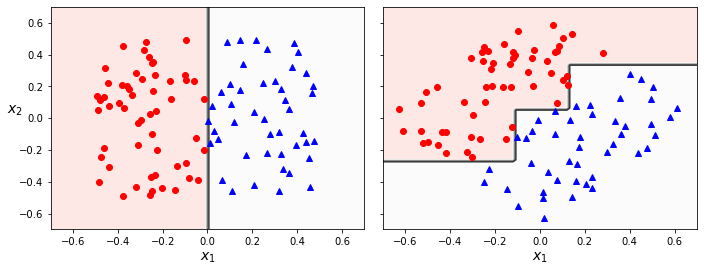
此外一点,就是决策树对于训练集上的某些异常样本异常敏感,可能仅仅是某几个样本,就会让生成的模型完全不一样。可以通过随机森林算法(random forest)来解决模型不稳定的问题。