Support Vector Machine
线性分类(Linear SVM Classification)
SVM基本定义
使用SVM进行分类,和传统的线性模型有何区别,可以从下图中得出答案
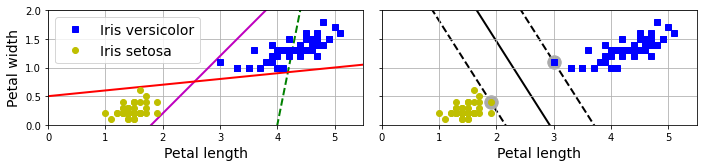
左边的图为使用三个线性模型进行分类的结果,其中虚线的模型无法正确分类,其他两个实线模型可以正确分类,不过其边界太靠近某些样本了,因此预测的时候很可能出错。
而右侧是使用SVM分类的结果,实现代表分类的分界线,可见SVM不仅可以正确的分类,而且尽量远离最接近的样本。SVM其实就是寻找两个样本之间的最宽的“大马路”(图中的虚线),因此也被称为大间距分类(large margin classification)。而虚线上圈起来的样本,称为支持向量(support vector)。
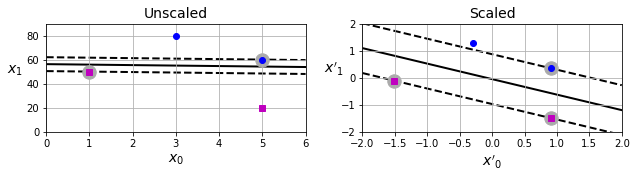
SVM对于特征的取值范围比较敏感,如下图所示。如果未经过特征缩放(feature scaling),x1的取值明显比x2要大,从而导致SVM的分类间距比较窄。经过特征缩放后,间距就比之前要宽很多。
软间隔分类(Soft Margin Classification)
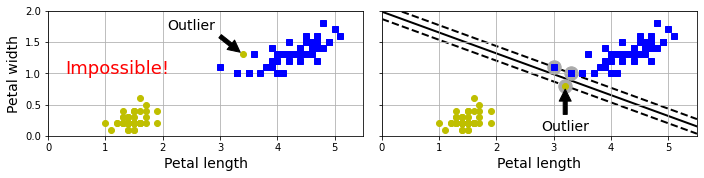
如果分类结果一定要非常准确,所有的样本一定要在正确的一侧,称之为硬间隔分类(hard margin classification)。但是这种硬性分类,就会存在两个问题,如下图所示
- 左图中,一个异常值就会导致模型无法线性分类
- 右图中,一个异常值会导致模型分类结果的间隔太窄
那么为了避免这种问题,就需要一个更加灵活的模型,可以在增加间距和允许误差(样本出现在虚线之内,甚至出现在错误的一侧)之间找到一个平衡,称之为软间隔分类(soft margin classification)。
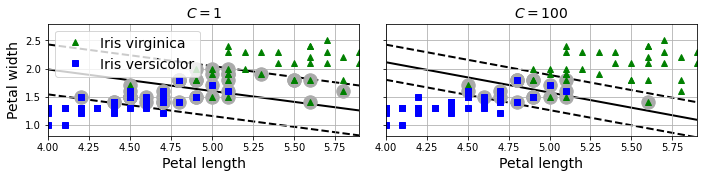
可以通过超参数C来控制这个度,越小的C就会允许更多的误差,从而让间隔更大,效果如下图所示
非线性分类(Nonlinear SVM Classification)
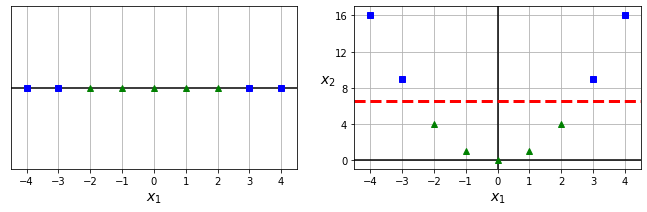
对于样本非线性分布的场景,可以类似第四章的做法,添加更多的特征(比如多项式特征),从而做到线性可分隔,如下图所示。之前的x1单一特征无法做到线性可分隔,添加了新特征x2=(x1)2后,就可以很容易分隔开来。
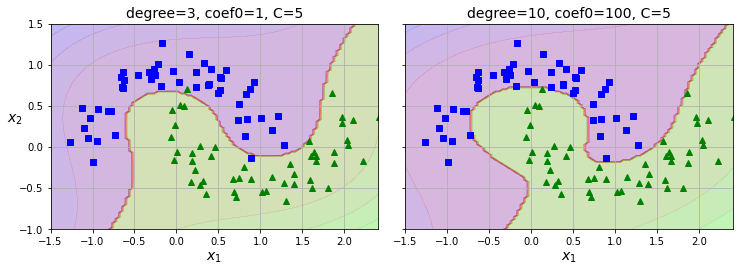
多项式核函数(Polynomial Kernel)
之前提到过,通过增加多项式特征,再用线性模型来拟合。但是问题依旧存在,项数少的模型简单,可能不足够拟合,而项数多的复杂模型又会增加计算量。
但是SVM有个比较神奇的特性,称之为kernel trick,能够在不实际增加多项式特征的情况下,得出相同的计算结果。因此即使项数较高,也不会导致特征数膨胀,因为并没有实际增加这些特征。
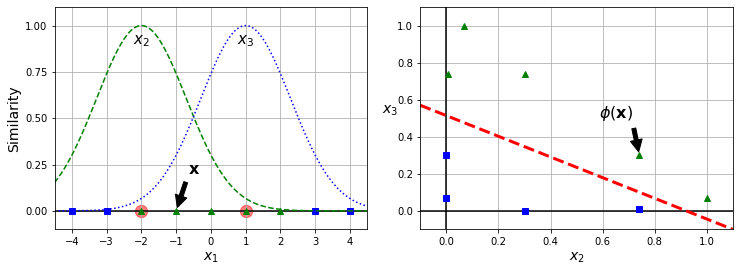
高斯核函数(Gaussian RBF Kernel)
处理非线性问题的另一个技巧,就是通过一个相似性函数来计算每个样本与指定的关键点的相似度,作为新增的相似性特征。
一个比较常见的函数,就是RBF(Gaussian Radial Basis Function,径向基核函数),其定义如下:
\phi\gamma(\mathrm{x},\ell)=\exp(-\gamma\|\mathrm{x}-\ell\|^2)这里的函数就是离目标越近取值越大。如下图所示,选择-2和1两个点作为目标,分别计算相似度函数的输出作为新的两个特征x2和x3。根据新的特征,就可以很容易找到分类之间的界限了。
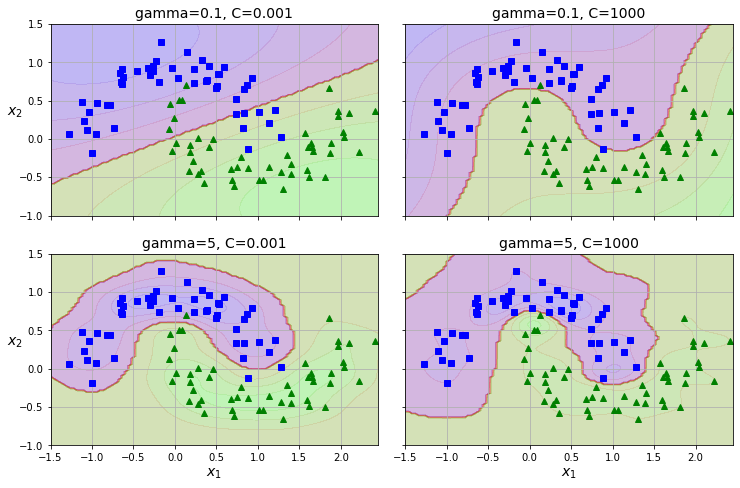
那么该如何挑选合适的关键点呢?最简单的做法就是每个样本都作为关键点,这样的话,每个样本都会增加很多特征。代价就是计算量会膨胀的厉害,比如之前m个样本,每个样本n个特征,处理后就会变成每个样本有m个特征。
还好有kernel trick,可以在不增加特征的前提下,得到相同的结果。比如下图,就是使用了SVC的rbf核,有两个超参数γ与C。C前面提到过,用来控制软间隔的度,C越小就允许越多的误差。γ则用来控制RBF曲线的宽度。γ越小,曲线越宽,关键点对其他样本的影响范围越大,分界线就越平滑。
计算复杂度
LinearSVC基于liblinear库,其实现了解决线性SVM的坐标下降算法(Coordinate Descent),但是并不支持kernel trick。其与样本数与特征数呈正比,计算复杂度大约为O(m * n)。
SVC基于libsvm库,其背后的算法为SMO算法(Sequential Minimal Optimization),且支持kernel trick。其计算复杂度大约在O(m2 * n)到O(m3 * n)之间,因此样本集很大的时候就会特别慢,所以比较适合模型很复杂但是样本数不大的训练集。
| Class | Time Complexity | Out-of-core | Scaling requied | Kernel trick |
|---|---|---|---|---|
| LinearSVC | O(m * n) | No | Yes | No |
| SGDClassifier | O(m * n) | Yes | Yes | No |
| SVC | O(m2*n) to O(m3*n) | No | Yes | Yes |
SVM回归
SVM不仅可以用于分类,也可以用于线性及非线性的回归。之前的分类,是找到一个最大的间距,间距中间尽量不出现样本。而回归的目标恰好相反,找到一个最小的间距,间距中间尽量覆盖所有的样本。间距的宽度由一个超参数ϵ来控制,ϵ越小宽度越小,因此有更多的样本不会出现在间距中。
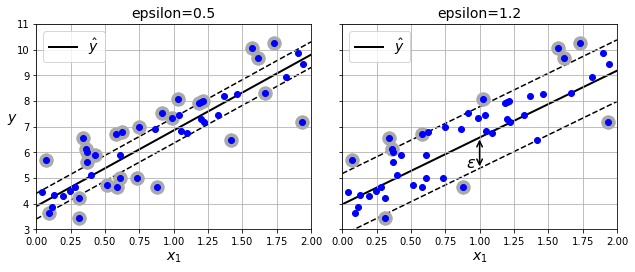
同样可以用于多项式模型的回归。除了之前的ϵ,还有一个超参数C用来控制正则化的度,C越大正则化度越小,曲线越能拟合更多的样本。如下图所示
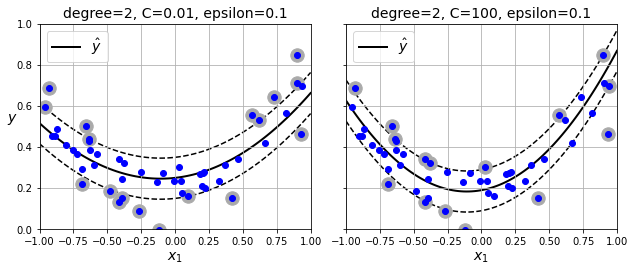
原理解析
决策函数及预测
线性SVM分类器用于预测时,对于一个样本x,其预测函数如下式所示
\hat{y}=\begin{cases}
0 &\text{if } \mathrm{w}^{T}\cdot\bold{x} + b < 0, \\
1 &\text{if } \mathrm{w}^{T}\cdot\bold{x} + b \ge0
\end{cases}下图为两维特征下用于分类的超平面,超平面与二维平面的交界线,就是前文图中的实线,实线上预测函数值为0。虚线就是函数值为1或者-1在二维平面的投影,虚线平行于实线,其构成的就是分类的间距。训练一个线性SVM模型,就是找到这样的w和b,让间距尽可能宽,并且让分类结果正确。
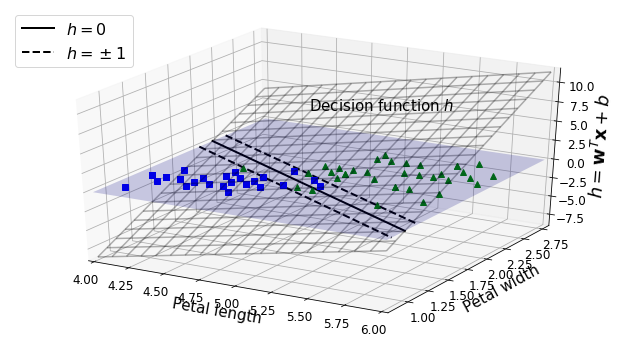
训练目标
训练函数的斜率等价于||w||,由于函数为1,斜率越小,其在二维平面的投影(也就是虚线)之间的间距也就越宽。下面一幅图就说明了斜率对于间距的影响。
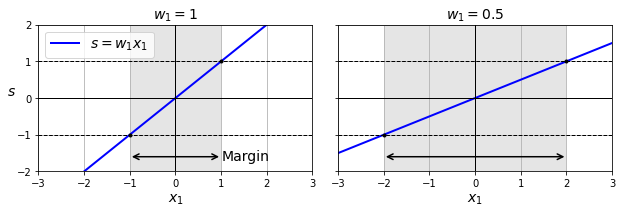
因此我们的训练目标就很明确了,一是让||w||尽量小,从而扩大间距,二是让样本分类尽量正确。分类正确的前提,就是positive样本函数值≥1,negtive样本函数值≤-1。
\begin{aligned}
t^{(i)}&=\begin{cases}
1 &\text{if } y^{(i)}=1 \\
-1 &\text{if } y^{(i)}=0
\end{cases}\\
\quad\\
对于&所有样本:
t^{(i)}(\bold{w}^{T}\cdot\bold{x}^{(i)} + b) \ge 1
\end{aligned}硬间隔分类目标
因此,在一定约束下找最优解的问题,称之为约束优化问题(constrained optimization problem)。对于硬间隔分类来说,其约束优化的目标定义如下
\begin{aligned}
&\min_{\bold{w}, b}&&\frac{1}{2}\bold{w}^T\cdot\bold{w} \\
&\text{subject to}&&t^{(i)}(\bold{w}^T\cdot\bold{x}^{(i)}+b) \ge 1 &\text{for}\ i=1,2,...,m
\end{aligned}这里的最小化目标,1/2 wTw,等价于1/2 ||w||2。至于为什么用l2-norm,而不是l1-norm,是因为求导就是简单的w,后续计算更方便。
软间隔分类目标
对于软间隔分类来说,每个样本增加ζ(i)参数,用来控制样本偏离的误差范围。其约束优化的目标定义如下
\begin{aligned}
&\min_{\bold{w}, b}&&\frac{1}{2}\bold{w}^T\cdot\bold{w} + C\sum_{i=1}^{m}\zeta^{(i)}\\
&\text{subject to}&&t^{(i)}(\bold{w}^T\cdot\bold{x}^{(i)}+b) \ge 1-\zeta^{(i)} &\text{for}\ i=1,2,...,m
\end{aligned}这里的超参数C,用来控制误差的度。根据优化函数,就可以看出C的作用了。C越大,样本偏差的影响越大,因此越不容易出现样本偏离。
对偶问题(The dual problem)
拉格朗日函数(Lagrange function)
对于一个约束优化问题,将约束条件移入优化目标,转化为无约束的优化问题。举例来说
\begin{aligned}
&\min_{x, y}&&f(x,y)=x^2 + 2y\\
&\text{subject to}&&3x+2y+1=0
\end{aligned}将约束条件乘上拉格朗日乘数,移入目标函数,变成新的拉格朗日函数(Lagrange function)
g(x,y,\alpha)=f(x,y)-\alpha(3x+2y+1)
拉格朗日证明,如果(x,y)为约束优化问题的一个解,则必定有一个α,使得(x, y, α)是拉格朗日函数的一个驻点(stationary point,函数在该点的一阶导数为零)。也就是说,计算出拉格朗日函数的驻点,则约束优化问题的解必定在这些驻点中。
\begin{cases}
\frac{\partial}{\partial{x}}g(x, y, \alpha)&= 2x-3\alpha\\
\quad\\
\frac{\partial}{\partial{y}}g(x, y, \alpha)&= 2-2\alpha\\
\quad\\
\frac{\partial}{\partial{\alpha}}g(x, y, \alpha)&= -3x-2y-1
\end{cases} \\
\quad\\
\hat{x}=\frac{3}{2}, \ \hat{y}=-\frac{11}{4}, \ \hat{\alpha}=1上述的结论,仅可用于相等式的约束。当然,在某些条件下(SVM符合这些条件),可以泛化到不等式。
拉格朗日对偶性(Lagrangian Duality)
假设某不等式约束条件下的优化问题如下定义
\text{min}\ f_0(x)\\
\text{subject to } f_{i}(x) \le 0 \quad \forall i \in 1, ..., m为了惩罚违反约束的样本,因此需要这么定义代价函数,当违反约束时代价最大化。
\begin{aligned}
J(x)=
\begin{cases}
f_0(x) &\text{if } f_i(x)\le 0,\\
\infty &\text{otherwise}
\end{cases}
\end{aligned}但是这个函数是不可微分的,所以用一个线性方程来替代,这个线性方程其实是原来方程的下界。
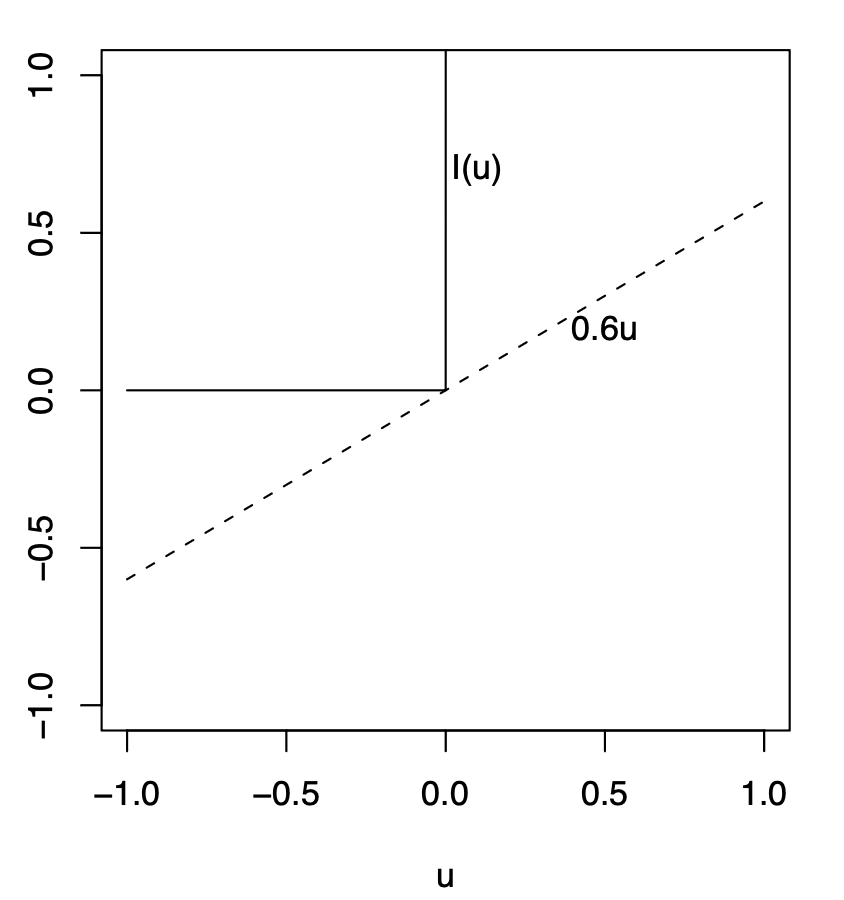
对应的拉格朗日函数为
L(x, \lambda)=f_0(x) + \sum_{i}\lambda_{i}f_i(x)因此,当所有的样本都符合约束时,L(x, 0) = f0(x);当有样本违反约束时,设置λ -> ∞,则L(x, λ) -> ∞。
\max_{\lambda}L(x, \lambda) = J(x) \\
\text{prime problem: }\quad\min_{x}\max_{\lambda}L(x, \lambda) \quad\quad\text{代价最小化}直接求解该问题非常复杂,因此可以调换下顺序,先对x求最小,再对λ求最大。对偶问题定义如下
\begin{aligned}
&\text{dual function: }&&g(\lambda)=\min_xL(x, \lambda)\\
&\text{dual problem: }&&\max_\lambda\min_xL(x, \lambda)=\max_\lambda g(\lambda)
\end{aligned}L(x, λ)对于x来说是一个仿射函数,而g(λ)又是该函数的极小值,因此对偶函数就是一个凹函数。求解minxL(x, λ)会比较困难,而对凹函数g(λ)求最大值,则会简单得多。
\begin{aligned}
&L(x, \lambda)\le J(x) && \forall\lambda\ge0\\
=>&\min_xL(x, \lambda)=g(\lambda)\le\min_x J(x) := p^*\\
=>&d^*=\max_\lambda g(\lambda)\le p^*
\end{aligned}d*就是原始问题的最优解,而p*为对偶问题的最优解。从上可以看出,g(λ)为原始问题最优解的下界,因此,对偶问题的求解,就是找到最靠近最优解时的λ值。
\max_\lambda\min_xL(x, \lambda) \le \min_{x}\max_{\lambda}L(x, \lambda)KKT条件
当d* <= p*时,称为弱对偶(weak duality)。当d* = p*时,称为强对偶(strong duality)。将p* – d*称为对偶间隙(duality gap)。
\begin{aligned}
f_0(x)&=g(\lambda) \\
&=\min_xL(x,\lambda)\\
&\le f_0(x) + \sum_{i}^{m}\lambda_{i}f_i(x) \\
&\le f_0(x) \\
=> \sum_{i}^{m}\lambda_{i}f_i(x) &= 0
\end{aligned}上式表明,当λi > 0 时,fi(x) = 0;当λi = 0 时,fi(x) < 0。
在SVM问题中,可以理解为支持向量的样本对应参数不为0,其他样本的参数为0。
SVM中的对偶问题
硬间隔分类的拉格朗日函数如下式所示,其中α(i)乘数,称之为KKT乘数,这些乘数必须不小于0。
L(\bold{w},b,\alpha)=\frac{1}{2}\bold{w}^T\cdot\bold{w}-\sum_{i=1}^{m}\alpha^{(i)}(t^{(i)}(\bold{w}^T\cdot\bold{x}^{(i)}+b)-1)\\
\text{with} \quad \alpha^{(i)}\ge0\quad\text{for}\ i=1,2,...,m同样,可以求w和b的偏微分,如下式所示
\frac{\partial}{\partial{\bold{w}}}L(\bold{w},b,\alpha)=\bold{w}-\sum_{i=1}^{m}\alpha^{(i)}t^{(i)}\bold{x}^{(i)}\\
\frac{\partial}{\partial{b}}L(\bold{w},b,\alpha)=-\sum_{i=1}^m\alpha^{(i)}t^{(i)}求偏微分为0时的驻点,则可以得出
\widehat{\bold{w}}=\sum_{i=1}^{m}\hat{\alpha}^{(i)}t^{(i)}\bold{x}^{(i)}\\
\sum_{i=1}^m\hat{\alpha}^{(i)}t^{(i)}=0将上述结果带入之前的拉格朗日函数,则可以得出SVM的对偶问题。
L(\bold{\widehat{w}},\hat{b},\alpha)= \sum_{i=1}^{m}\alpha^{(i)} - \frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha^{(i)}\alpha^{(j)}t^{(i)}t^{(j)}\bold{x}^{(i)T}\cdot\bold{x}^{(j)}\\
\text{with} \quad \alpha^{(i)}\ge0\quad\text{for}\ i=1,2,...,m \\
\quad\\
对偶问题:\max_{\alpha}L(\bold{\widehat{w}},\hat{b},\alpha)现在目标就是要找到这样的向量α,从而继续求出w和b。
\begin{aligned}
\widehat{\bold{w}}&=\sum_{i=1}^{m}\hat{\alpha}^{(i)}t^{(i)}\bold{x}^{(i)}\\
t^{(i)}&(\bold{w}^{T}\cdot\bold{x}^{(i)} + b)=1 \\
\quad\\
&对于样本k\\
\hat{b}&=1-t^{(k)}(\widehat{\bold{w}}^{T}\cdot\bold{x}^{(k)})\\
&所有样本取均值\\
\hat{b}&=\frac{1}{n_s}\sum_{i=1}^m\left[1-t^{(i)}(\widehat{\bold{w}}^{T}\cdot\bold{x}^{(i)})\right]\\
&\text{subject to} \ \hat{\alpha}^{(i)}>0
\end{aligned}Kernelized SVM
前文提到的二项式模型,需要将原始样本集映射到核函数计算后的训练集。一个典型的二项式核函数定义如下
\phi(\bold{x})=\phi\bigg(\dbinom{x_1}{x_2}\bigg)
=
\begin{pmatrix}
{x_1}^2\\
\sqrt{2}x_1 x_2\\
x_2
\end{pmatrix}
2维向量空间映射为3维向量空间,如果两个映射后的向量进行点积,结果如下
\begin{aligned}
\phi(\mathrm{a})^T\cdot\phi(\mathrm{b}) &=
{
\begin{pmatrix}
{a_1}^2\\
\sqrt{2}a_1 a_2\\
{a_2}^2
\end{pmatrix}
}^T
\cdot
\begin{pmatrix}
{b_1}^2\\
\sqrt{2}b_1 b_2\\
{b_2}^2
\end{pmatrix}
=
{a_1}^2{b_1}^2+2a_1 b_1 a_2 b_2+{a_2}^2{b_2}^2 \\
&=(a_1 b_1+a_2 b_2)^2 \\
&=\bigg(
\dbinom{a_1}{b_1}^T\cdot\dbinom{b_1}{b_2}
\bigg)^2\\
&=(\mathrm{a}^T\cdot\mathrm{b})^2
\end{aligned}也就是说映射后的向量点积,等价于原始的向量点积。也就说,将训练集通过核函数映射到高维空间,点积后的结果等价于原始向量的点积。因此就无需映射到高维空间,从而避免了大量的计算,这就是kernel trick的精髓。
K(a, b) = (aT . b)2,就是二项式核。在机器学习中,如果一个函数ϕ具体这样的特性,两个函数的点积结果等价于原始向量的点积,不用实际进行函数的映射,这样的函数称为核函数(kernel)。常用的核函数如下:
\begin{aligned}
线性核:&&K(\bold{a},\bold{b})&=\bold{a}^T\cdot\bold{b}\\
多项式核:&&K(\bold{a},\bold{b})&=(\gamma\bold{a}^T\cdot\bold{b} + r)^d\\
高斯核:&&K(\bold{a},\bold{b})&=\text{exp}(-\gamma\|\bold{a}-\bold{b}\|^2)\\
\text{Sigmoid}核:&&K(\bold{a},\bold{b})&=\text{tanh}(\gamma\bold{a}^T\cdot\bold{b}+r)\\
\end{aligned}将SVM模型用于预测时,通过核函数计算w的时候,ϕ(x(i))的计算量会特别大。利用核函数的特性,可以避免大计算量的运算,原理如下:
\begin{aligned}
h_{\widehat{w}, \hat{b}}(\phi(\bold{x}^{(n)}))&=\widehat{\bold{w}}^T\cdot\phi(\bold{x}^{(n)}) + \hat{b}\\
&=(\sum_{i=1}^m\hat{\alpha}^{(i)}t^{(i)}\phi(\bold{x}^{(i)}))^T\cdot\phi(\bold{x}^{(n)}) + \hat{b}\\
&=\sum_{i=1}^m\hat{\alpha}^{(i)}t^{(i)}(\phi(\bold{x}^{(i)})^T\cdot\phi(\bold{x}^{(n)}) + \hat{b}\\
&=\sum_{i=1}^m\hat{\alpha}^{(i)}t^{(i)}K(\bold{x}^{(i)}, \bold{x}^{(n)}) + \hat{b}\\
&\text{subject to} \ \hat{\alpha}^{(i)}>0
\end{aligned}α != 0时的样本为支持向量,因此对于x(n)求预测值时,仅需要计算该样本与支持向量的点积,而无需计算全部的训练样本。当然,还需要计算bias term,过程如下
\begin{aligned}
\hat{b} &= \frac{1}{n_s}\sum_{i=1}^m\left[1-t^{(i)}\widehat{\bold{w}}^{T}\cdot\phi(\bold{x}^{(i)})\right]\\
&= \frac{1}{n_s}\sum_{i=1}^m\left[1-t^{(i)}\bigg(\sum_{j=1}^m\hat{\alpha}^{(j)}t^{(j)}\phi(\bold{x}^{(j)})\bigg)^T\cdot\phi(\bold{x}^{(i)})\right]\\
&= \frac{1}{n_s}\sum_{i=1}^m\left[1-t^{(i)}\sum_{j=1}^m\hat{\alpha}^{(j)}t^{(j)}K(\bold{x}^{(i)},\bold{x}^{(j)})\right]\\
&\text{subject to} \ \hat{\alpha}^{(i)}\gt0, \hat{\alpha}^{(j)}\gt0,
\end{aligned}