Classification
分类模型评价指标
混淆矩阵(Confusion Matrix)
首先,仅仅看准确率是远远不够的。以书中的数字识别为例,一共10个数字,即使用一个非常简单的“数字5分类器”(永远返回false),也会有90%左右的准确率,因为验证集中数字5仅占比10%。
混淆矩阵就是将分类结果划分为4个象限,如下图所示:
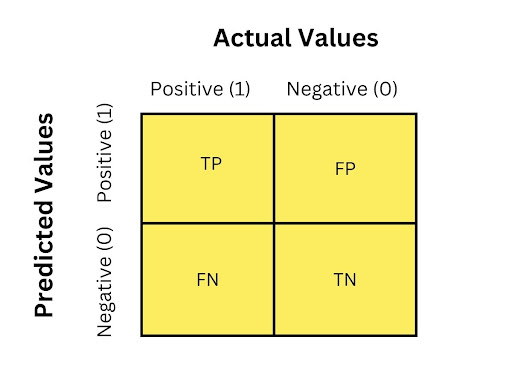
- TP:True Positive,识别出来的正确结果(判断正确)
- FP:False Positive,识别出来的错误结果(判断错误)
- TN:True Negtive,未识别到的错误结果(判断正确,应该排除)
- FN:False Negtive,未识别到的正确结果(未识别到,遗漏)
一个完美的分类器,应该只有TP和TN,FP和FN都为0。准确率就是评估结果中正确结果占比,也就是水平第一行中的TP占比。
precision = \frac{TP}{TP + FP}但是上文提到,仅有准确率是不够的。假如一个分类器仅能正确识别1个True,其他都识别为False,那么准确率也是100%。
因此,引入了另一个指标,召回率(Recall, sensitivity,true positive rate/TPR),评估所有正确结果中被找到的占比,也就是第一列中TP的占比。
recall = \frac{TP}{TP + FN}Precision and Recall
F1 Score
为了方便评估,将两个指标组成1个指标,就是F1 Score。F1 Score就是两个指标的调和平均数(harmonic mean),调和平均数的定义如下:
\frac{1}{H} = \frac{(1/x_1) + (1/x_2)}{2} F1 Score的定义如下所示:
F_1 = \frac{2}{\frac{1}{precision} + \frac{1}{recall}} = 2 \times \frac{precision \times recall}{presion + recall} = \frac{TP}{TP + \frac{FN + FP}{2}}Precision与Recall的权衡
大部分分类器的结果,是一个得分或者说概率,得分高于某个阈值则识别为positive,否则识别为negtive。这个阈值的调整,会导致precision和recall的变化,如下图所示:
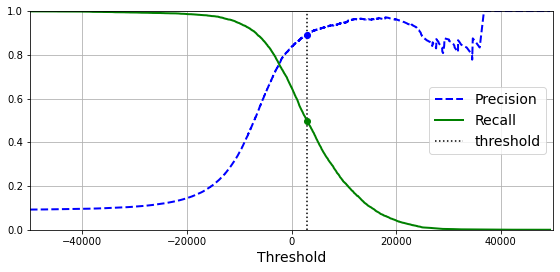
当阈值提高的时候,准确率会提升,但是会导致误判很多正确的case,recall就会降低。注意到这里的precision随着阈值提升,还会有向下的抖动。这是因为precision从 n/m 变成了 (n-1)/(m-1),所以有所降低。
还有一种找到最佳阈值的办法,就是用一条变化曲线来呈现两个指标,如下图所示:
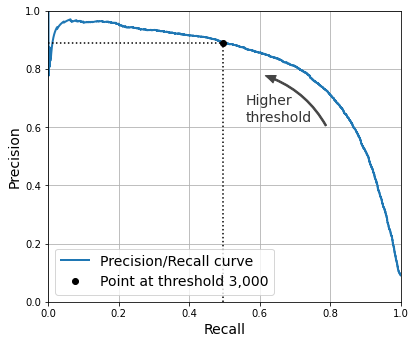
ROC曲线
ROC曲线,与上文中的图类似,两个坐标轴的值是TPR(true positive rate,也就是recall)与FPR(false positive rate)。
TPR = \frac{TP}{TP + FN} \qquad FPR = \frac{FP}{FP + TN}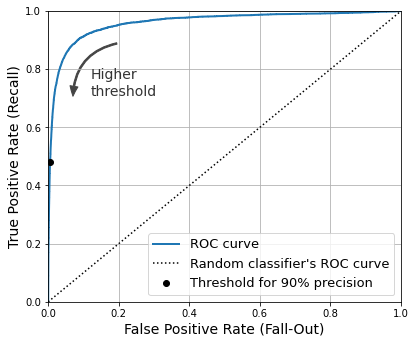
同样,阈值越高,越容易过滤掉正确的结果,从而导致TPR下降,而此时结果中准确率很高,就不会有太多的误判,因此FPR也会下降。一个好的分类器,应该尽可能让结果靠近左上角,高TPR低FPR。
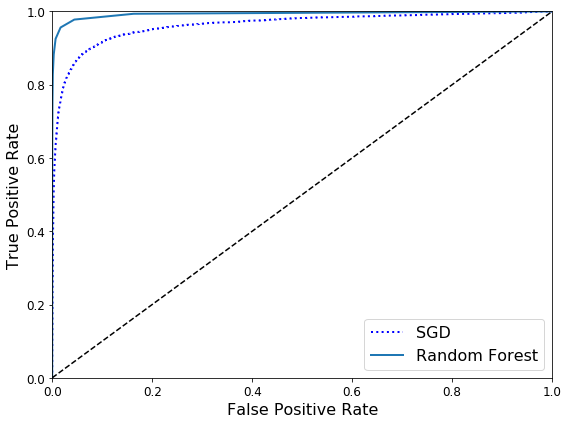
如何比较两个分类器的结果呢?可以用一个指标AUC(area under the curve)来评价,就是曲线下面的面积的占比,好的分类器会接近1。如下图所示,Random Forest表现就比SGD更好。
多元分类(Multiclass Classification)
之前的分类器都是二元分类(比如SVM或者线性分类),有一些算法是可以处理多元分类(比如Random Forest或者naive Bayes)。当然,也可以用多个二元分类器来实现多元分类的效果。
one-versus-all(OVA)
10个数字,每个数字启用一个专门的二元分类器,每次分类从10个分类器结果中,挑选一个得分最高的分类器,就是最终的分类结果。
这个策略的好处,就是总的分类器有限,识别成本较小。
one-versus-one(OVO)
另一种做法,就是每个分类器都用来区分2个分类结果,比如一个分类器用来区分0和1,一个分类器用来区分0和2。所以如果有N个分类,那么就需要准备N * (N-1) / 2个分类器。上文中10个数字的识别,就需要45个分类器。最终的结果,就是看哪个数字赢的最多。
这个策略的优势,在于训练数据的时候,仅需要两个分类结果的训练集,而不需要全部训练集。
有些算法,比如SVM,训练集越大耗时越长。因此对于SVM这类算法,OVO训练时间更短,是比较适合的场景。其他算法的话,默认使用OVA策略。
多标签分类(Multilabel Classification)
多标签分类,指的是一个样本输出多个标签。有些分类算法,比如KNeighborClassifier,是支持多标签分类的。
评估分类结果的时候,每个标签都计算F1 Score,然后多个标签最后计算平均值即可。
多输出分类(Multioutput Classification)
多输出分类,其实是多标签分类的一种泛化,就是说一个样本输出多个标签,而每个标签又可以有多个取值。比如数字识别,可以输出多个标签(每个像素点一个标签),同时每个标签有多个取值(从0~255的像素值)。